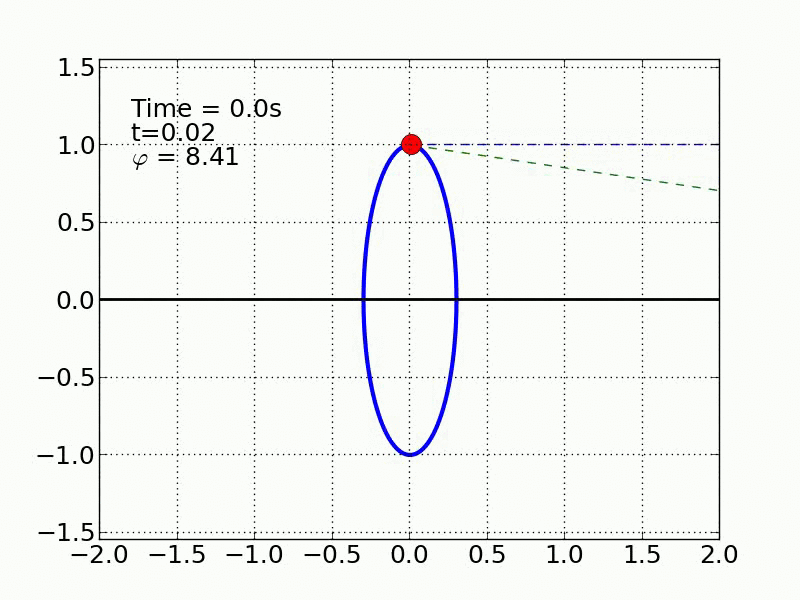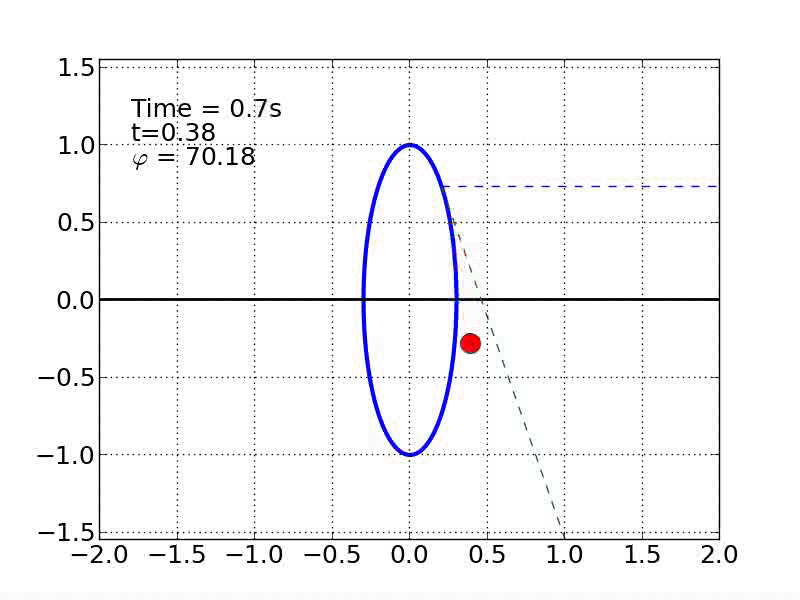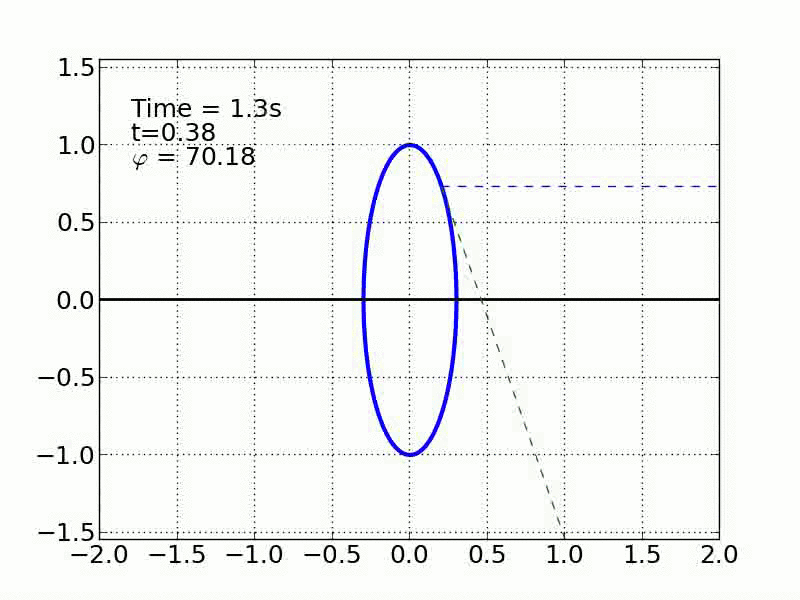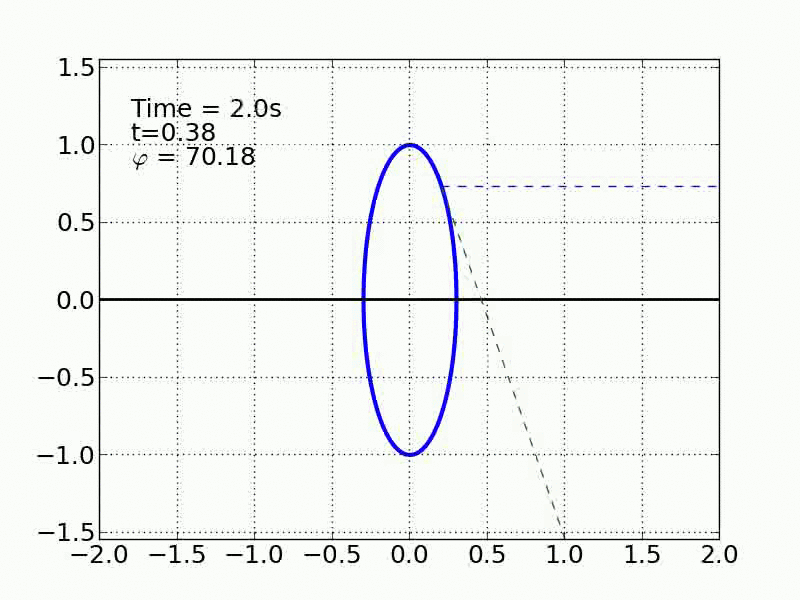
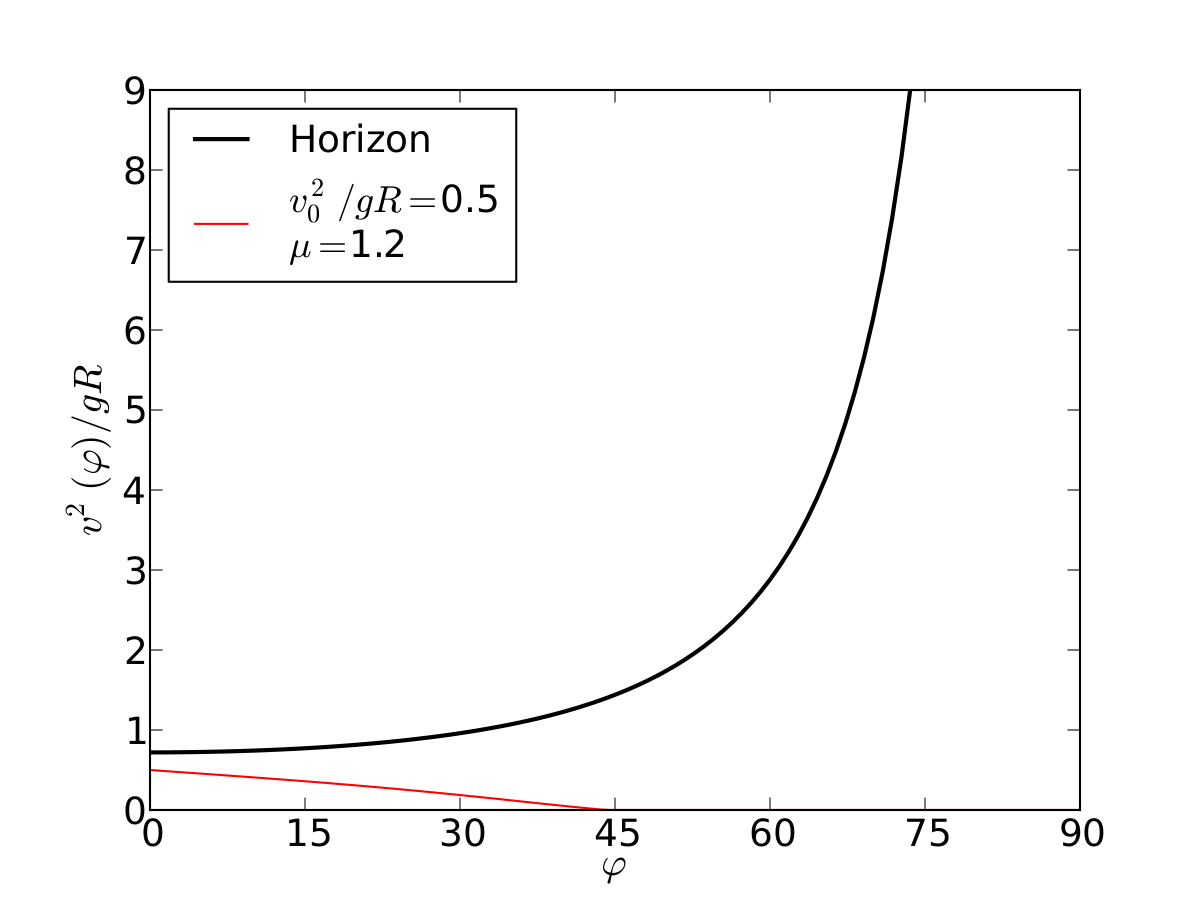
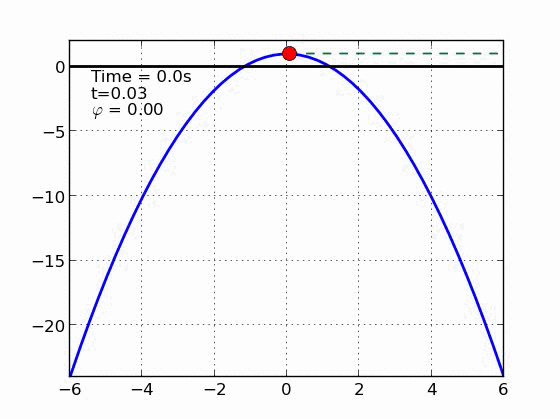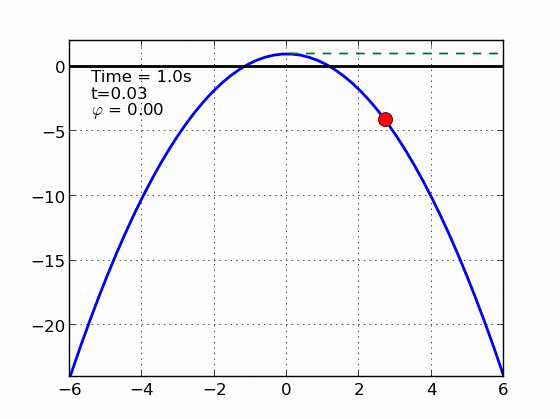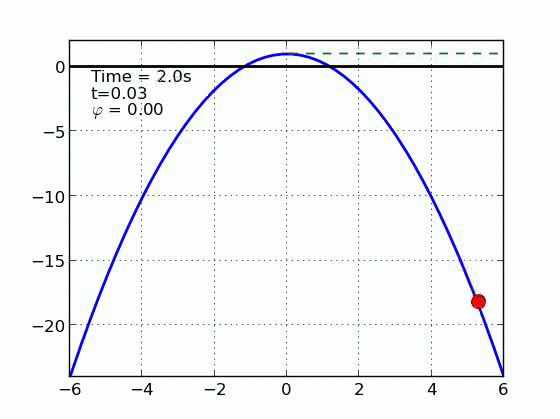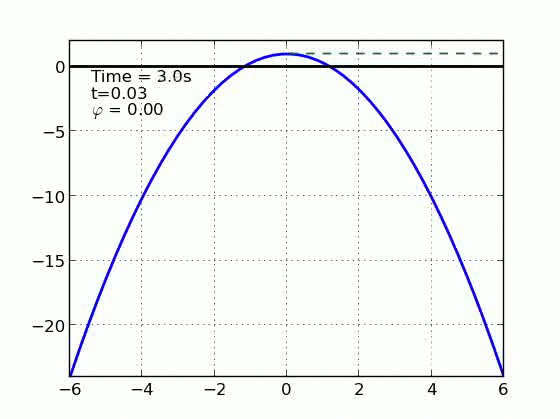
Sliding With Friction
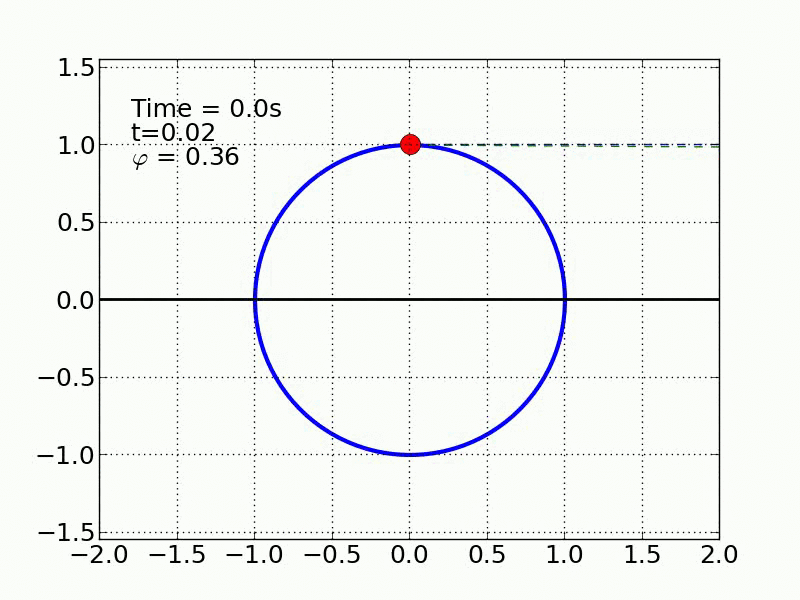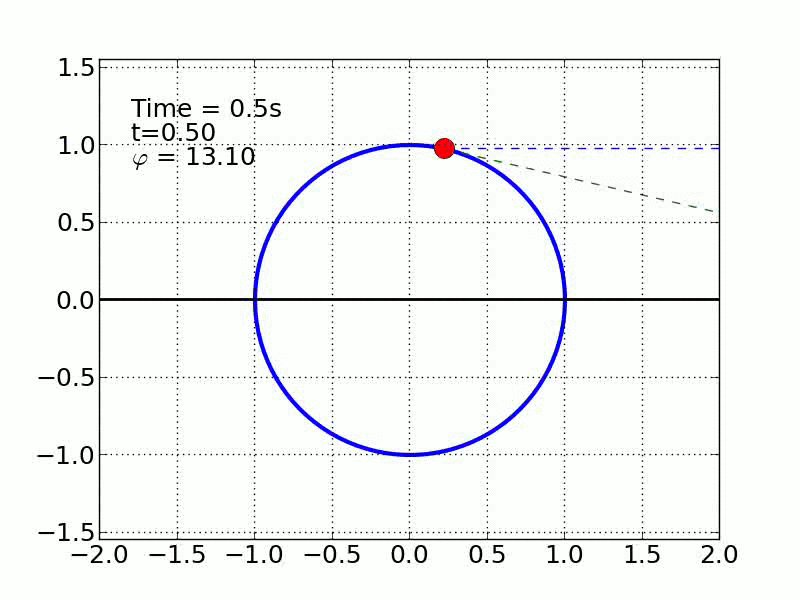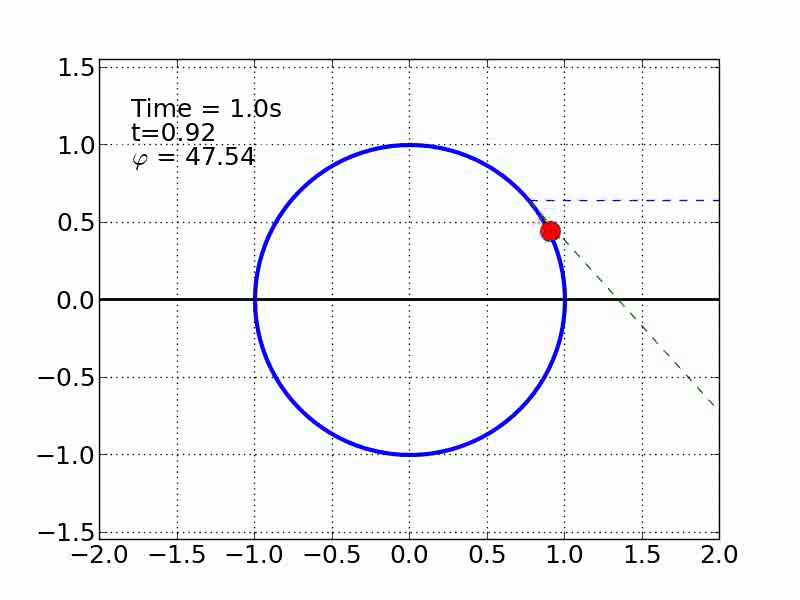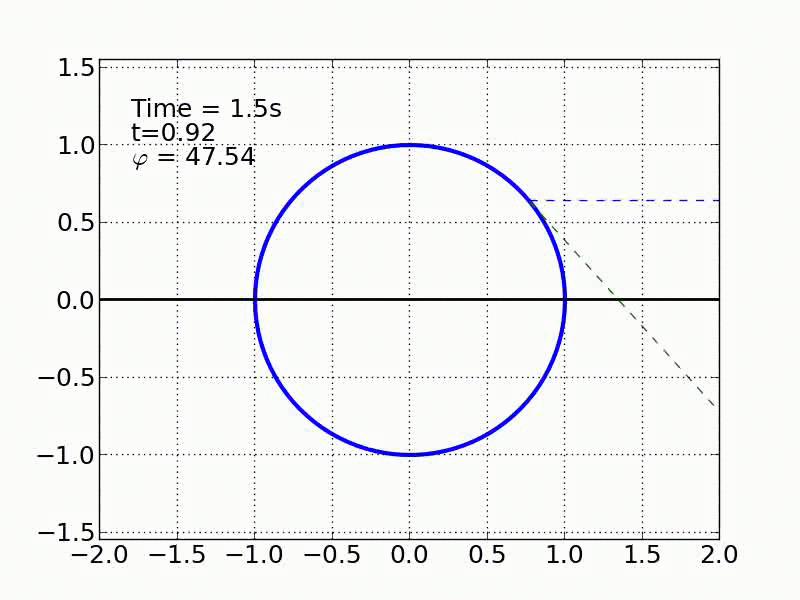
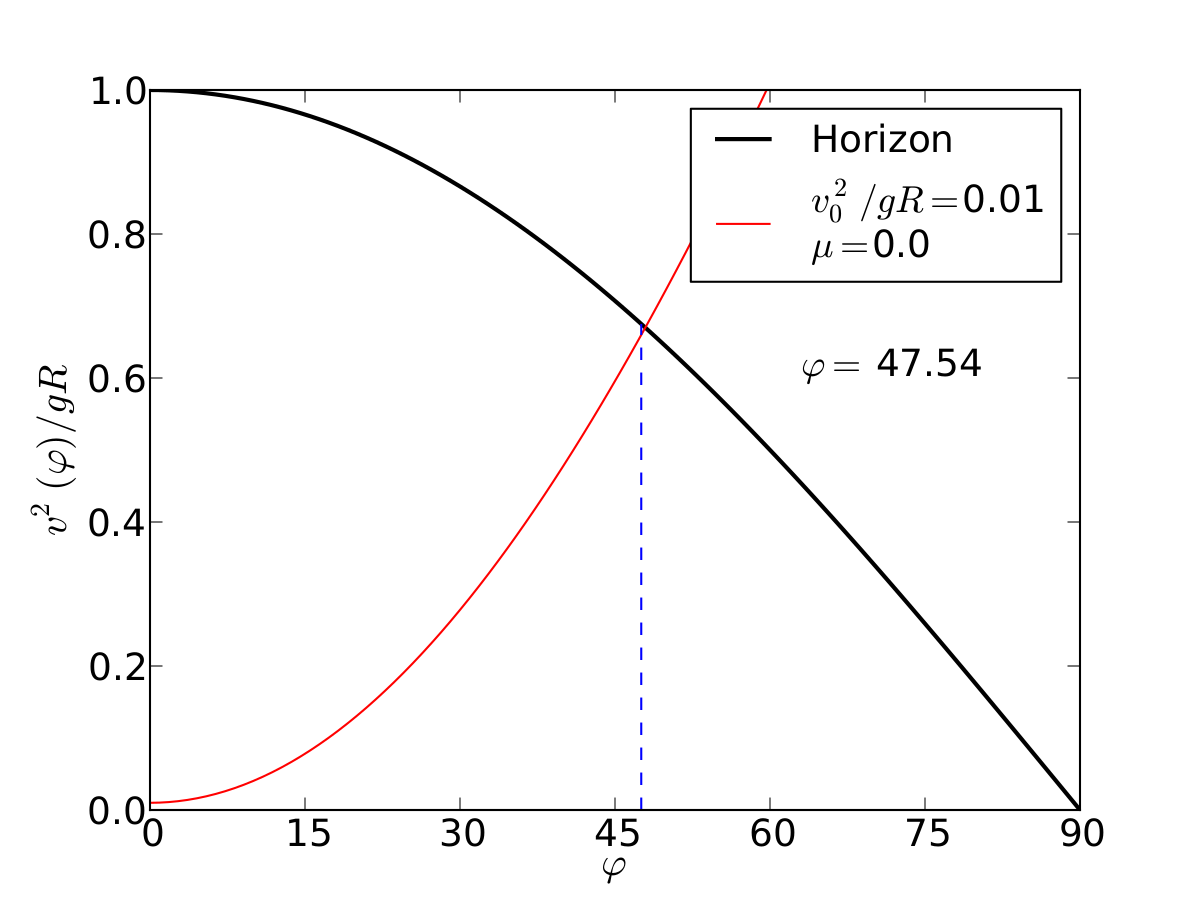
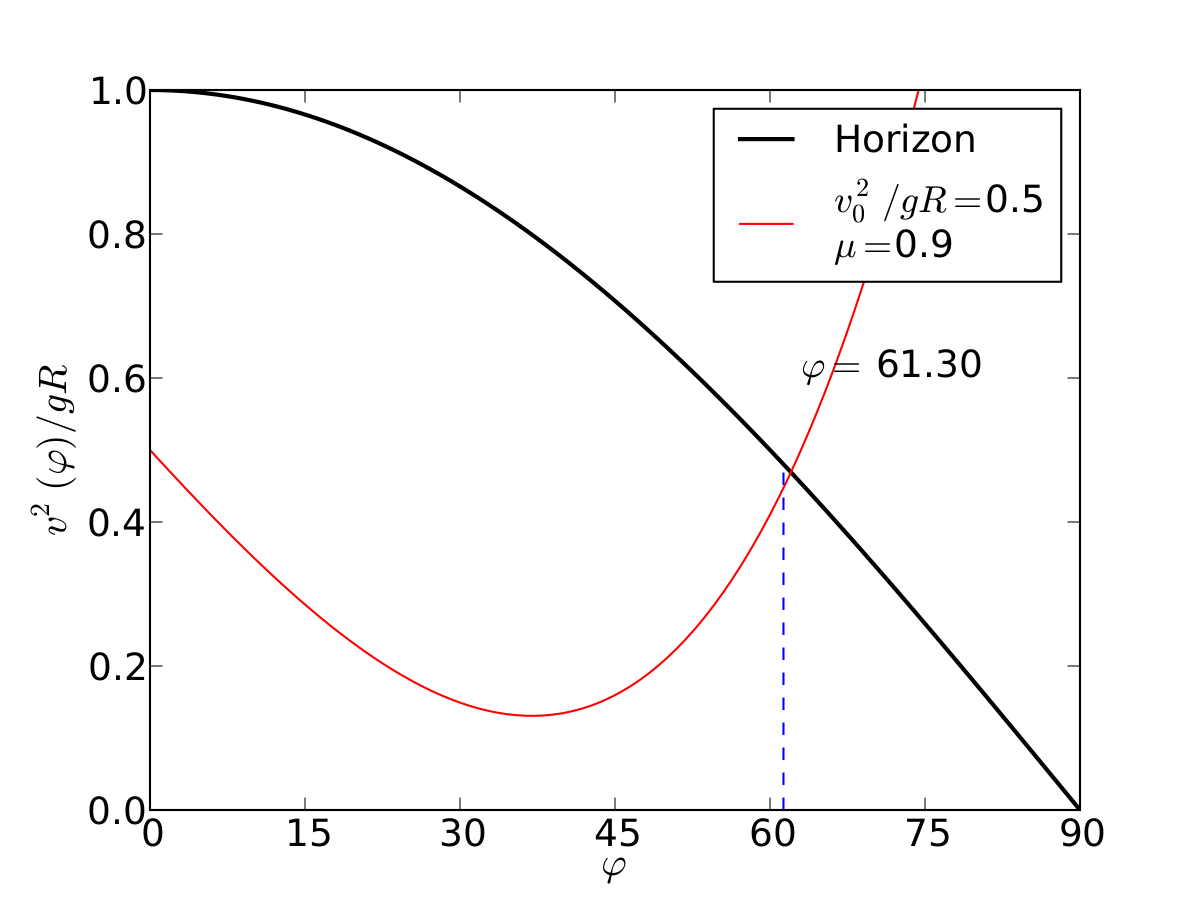
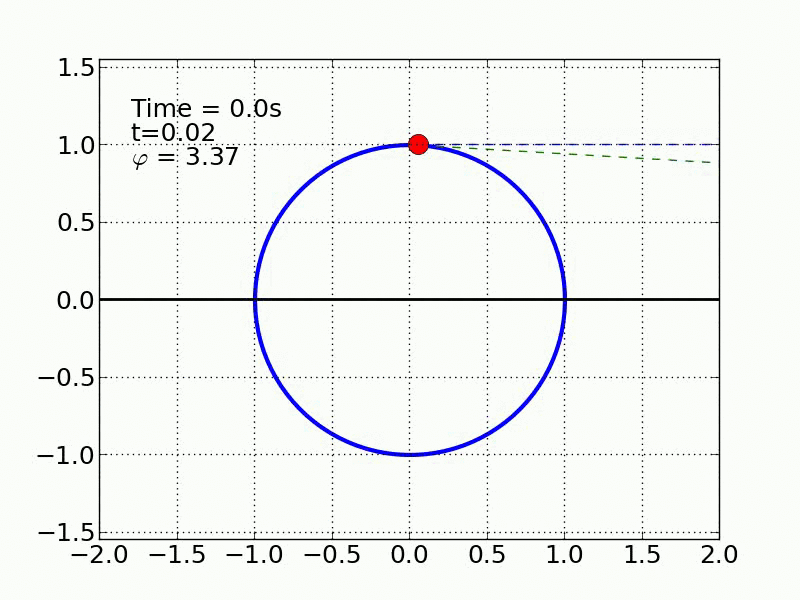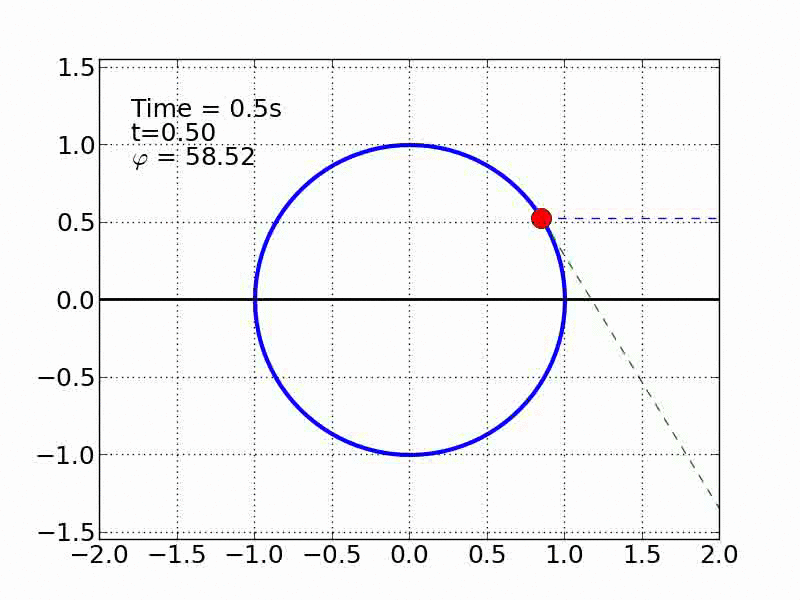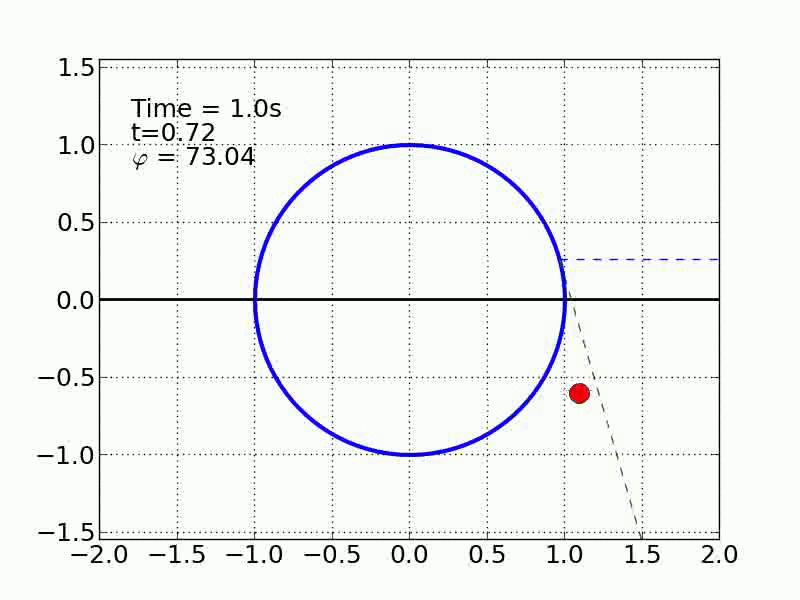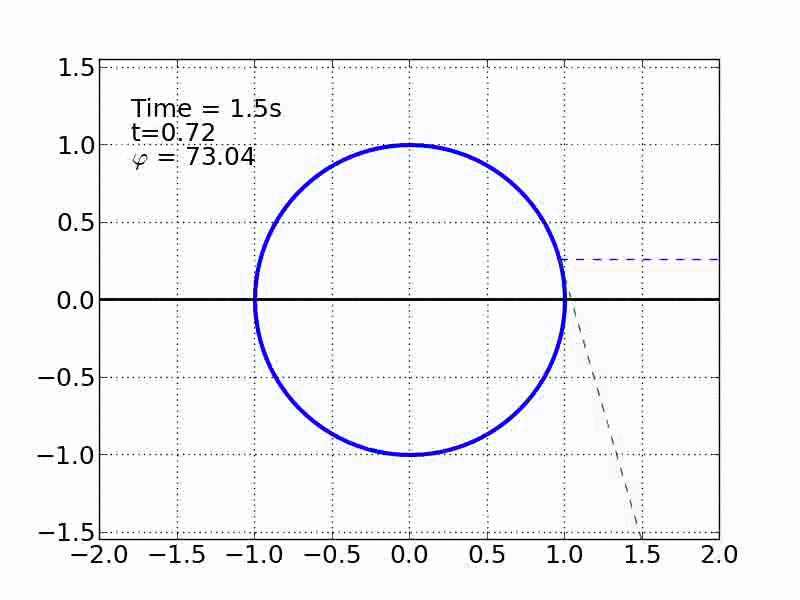
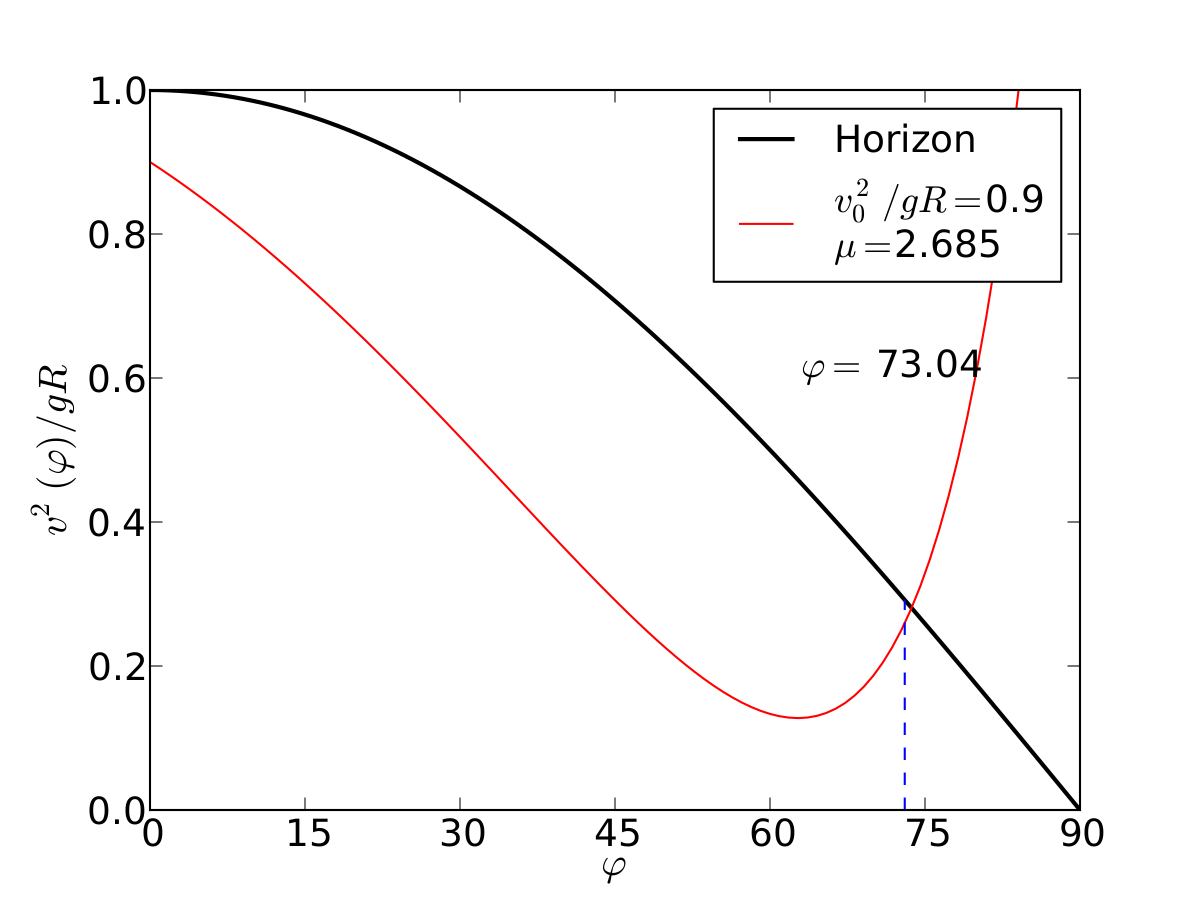
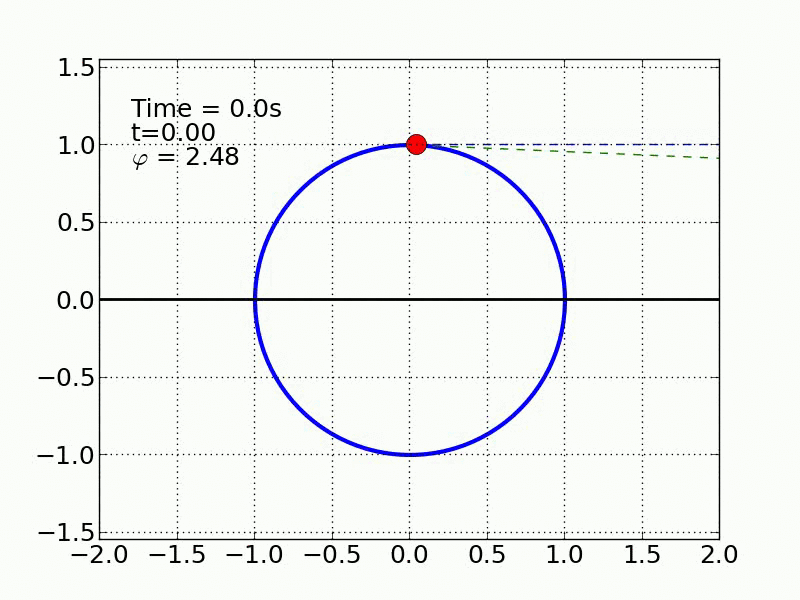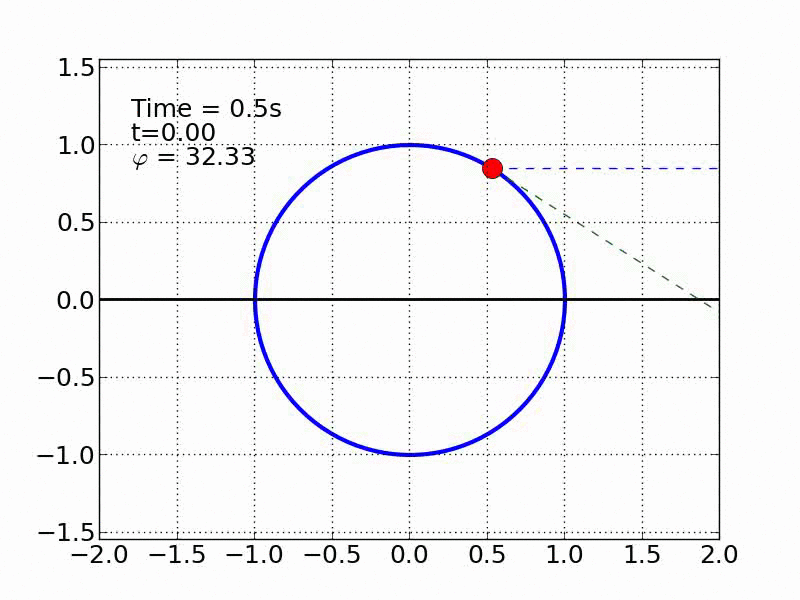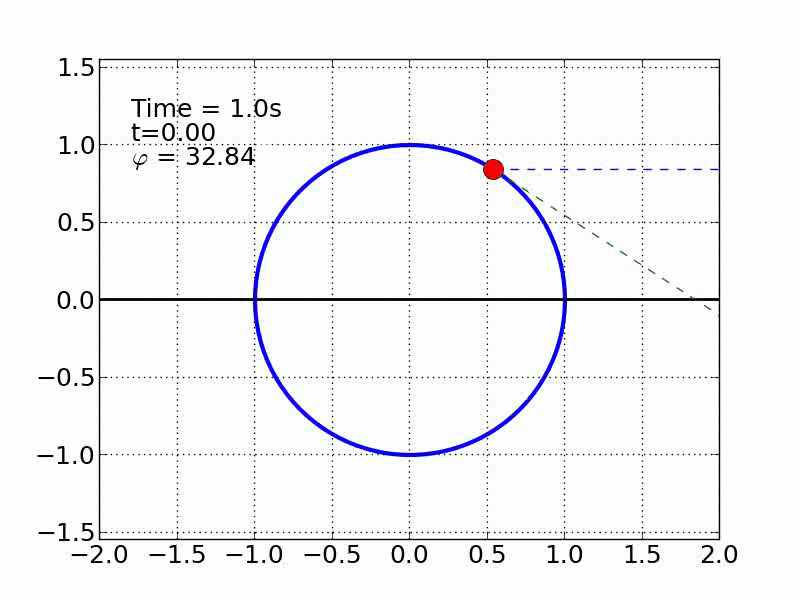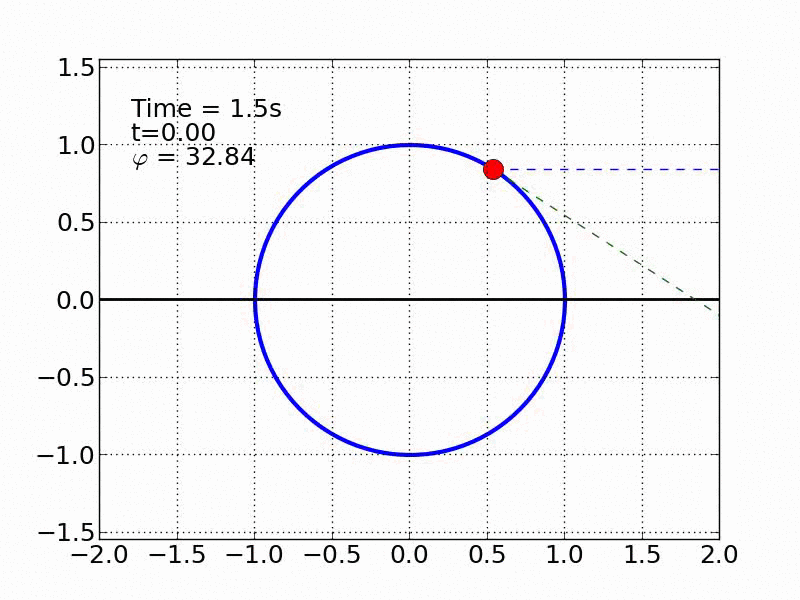
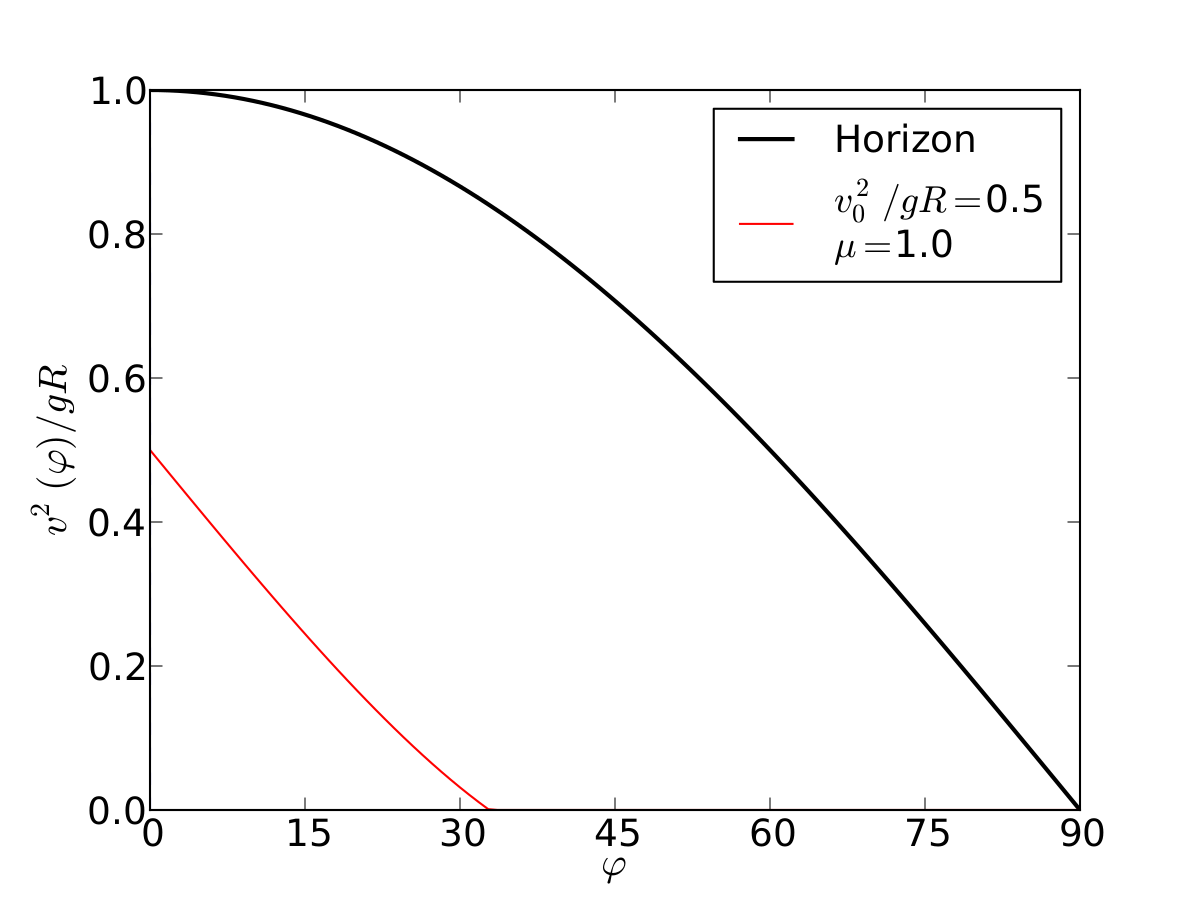
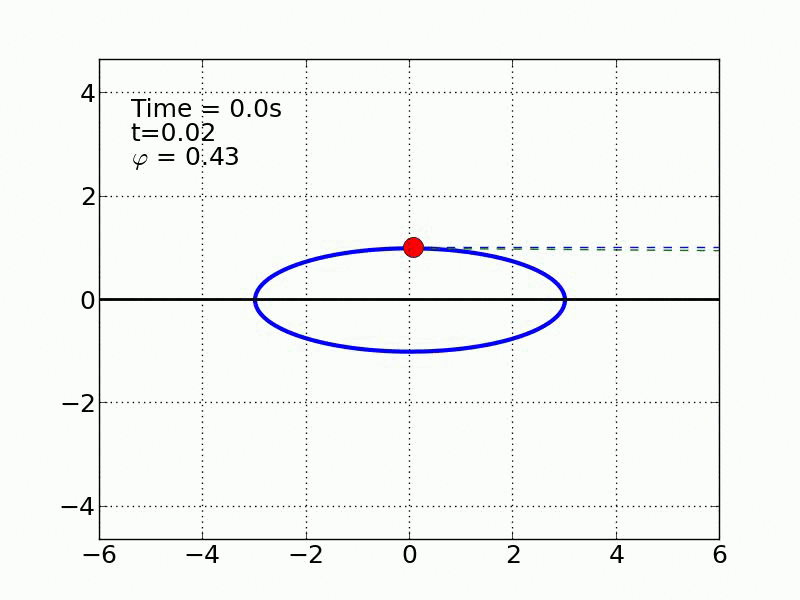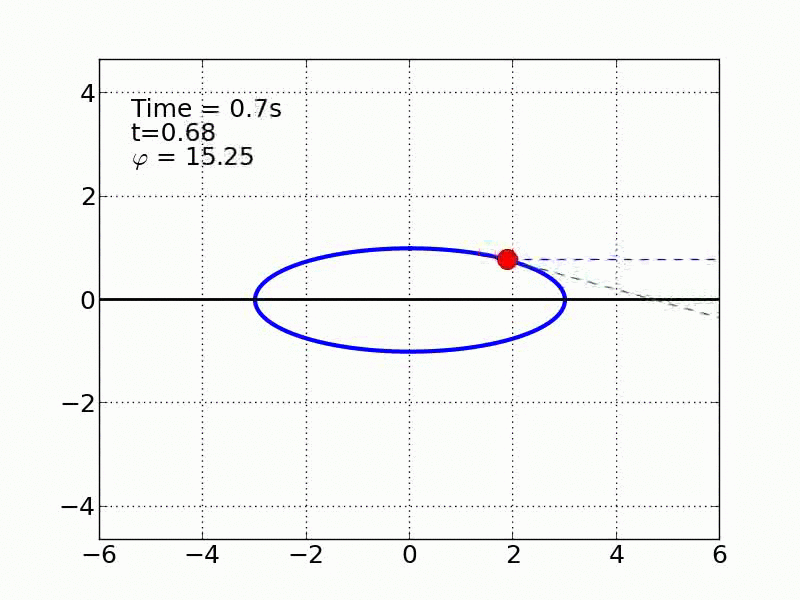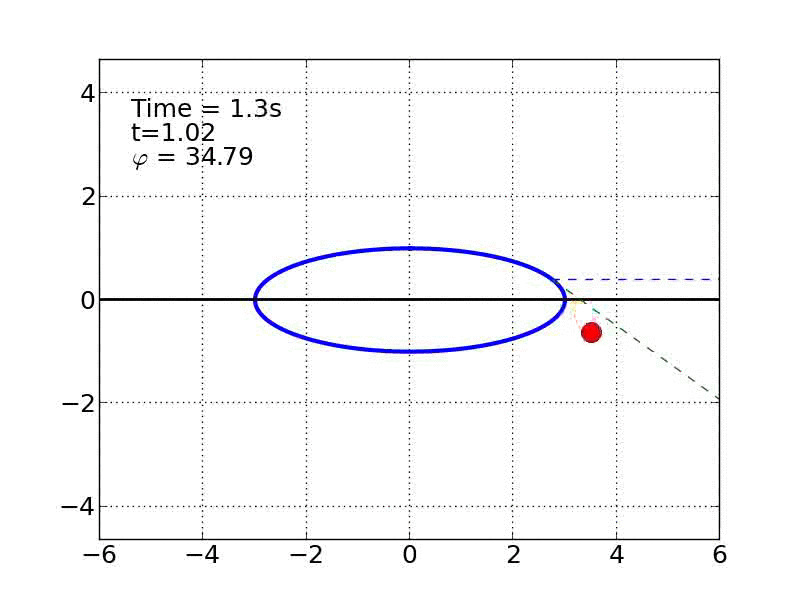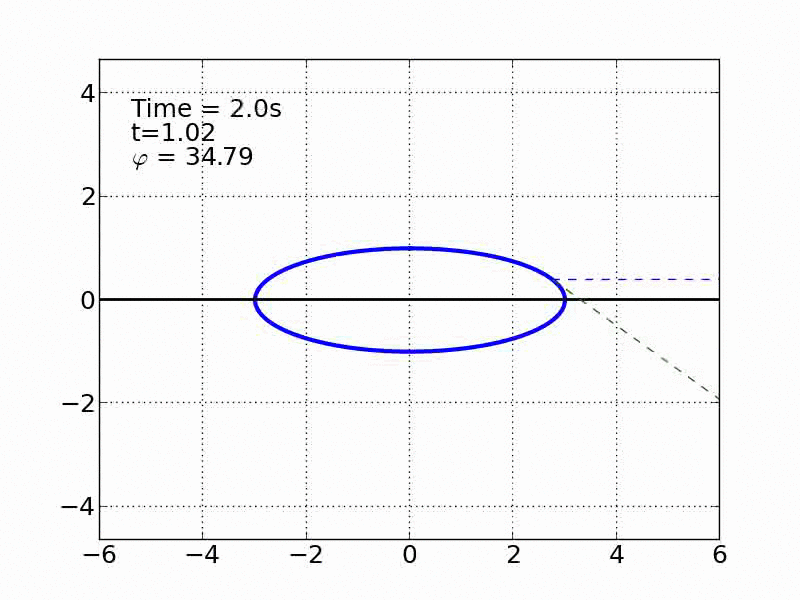
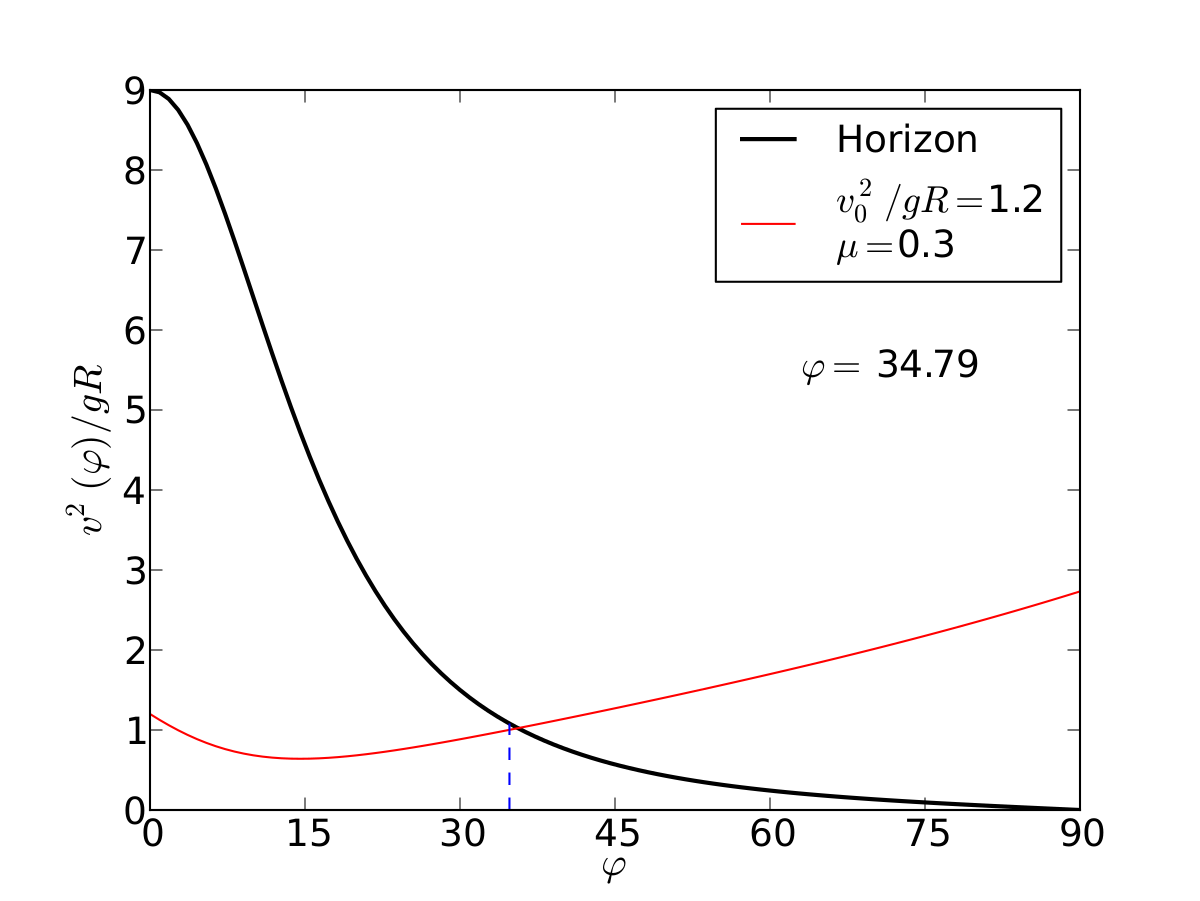
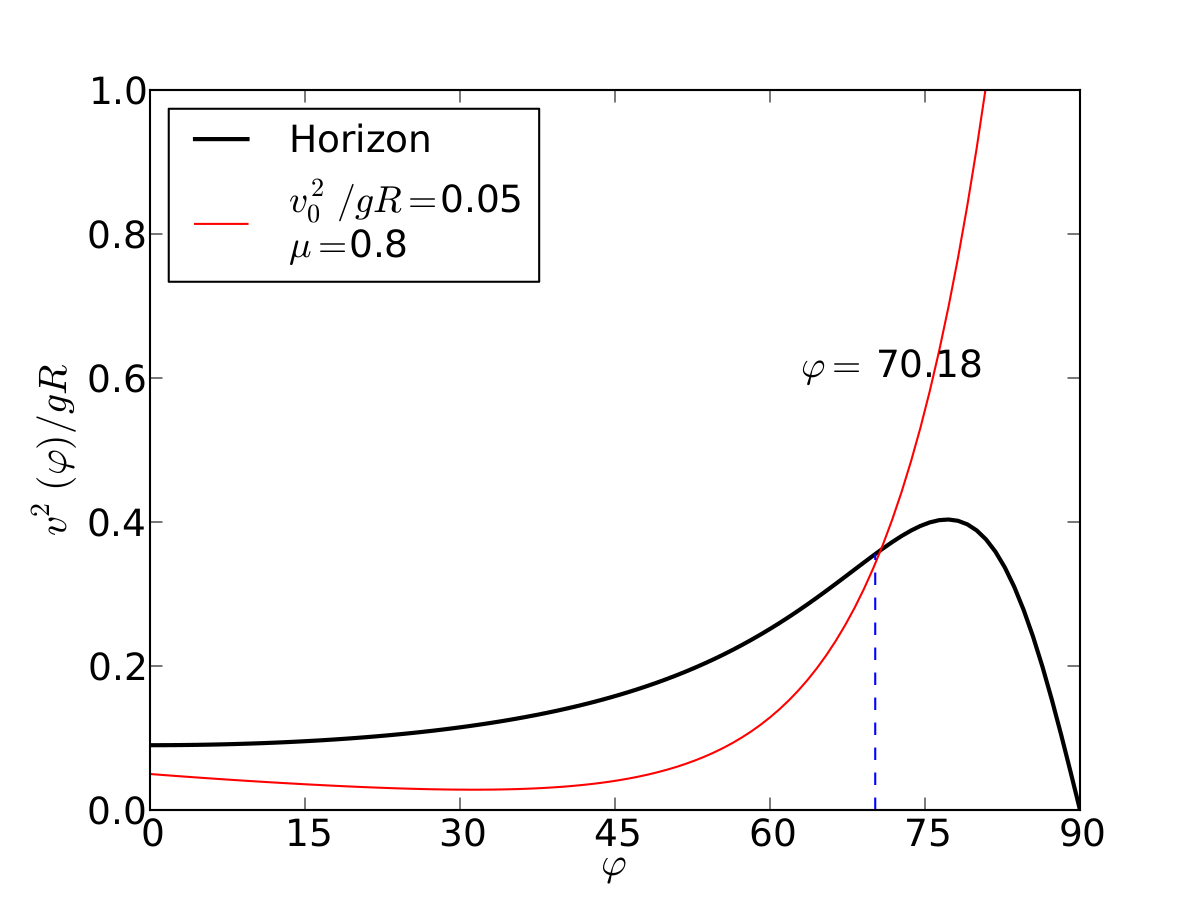
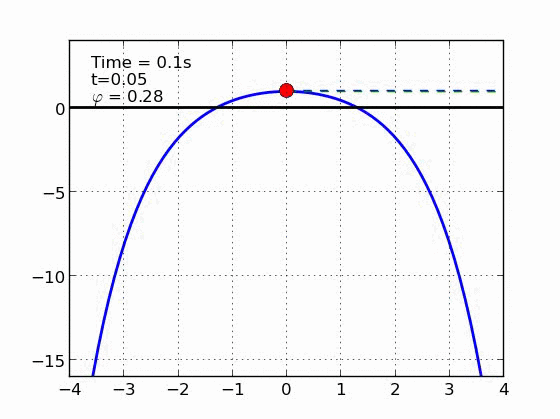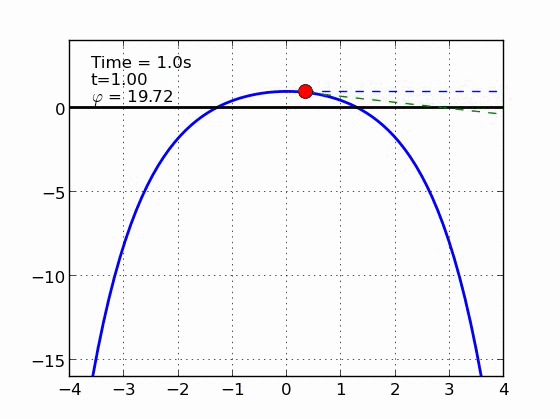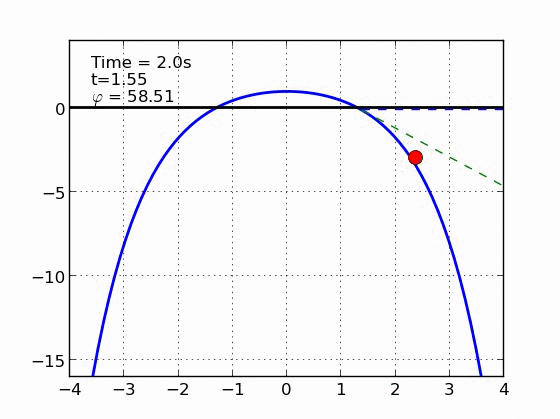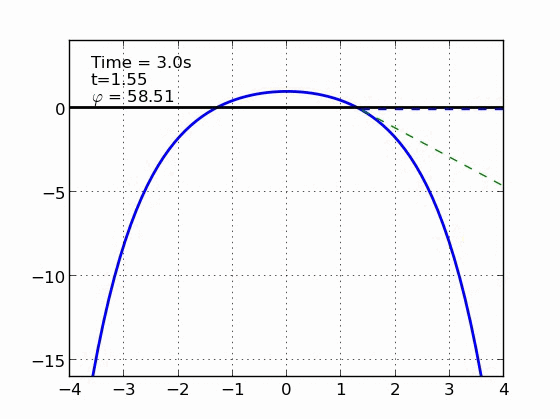
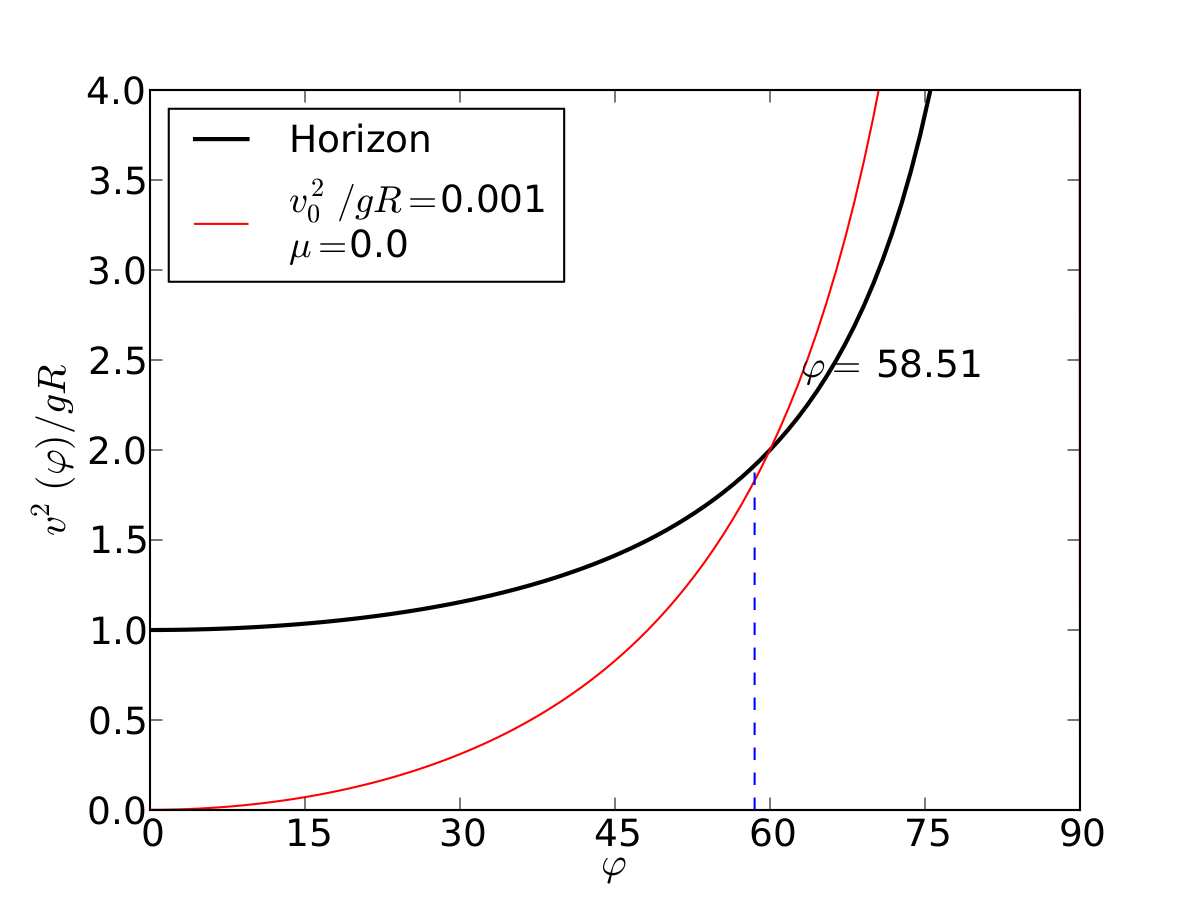
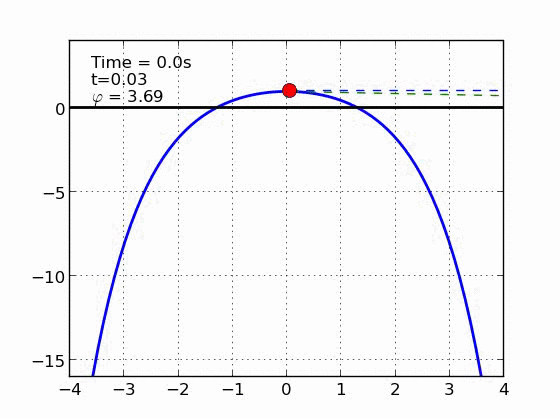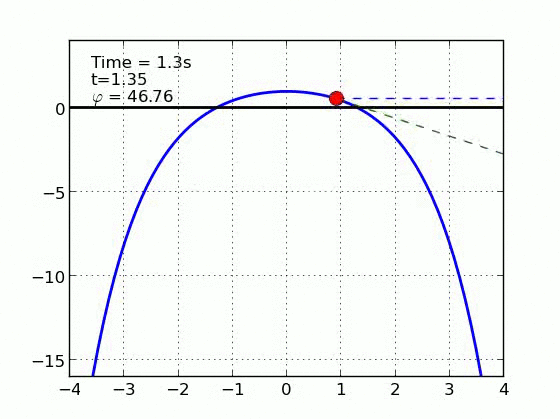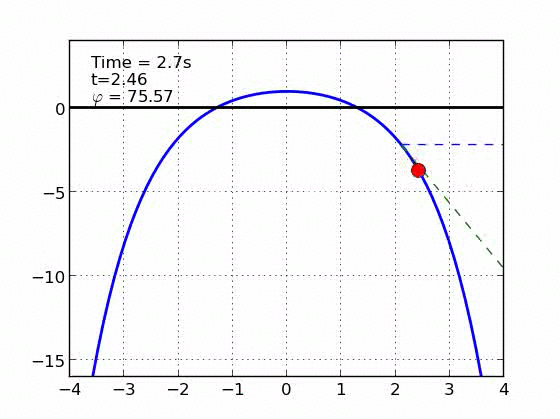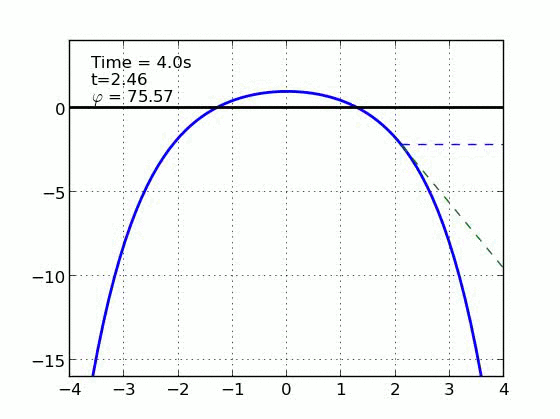
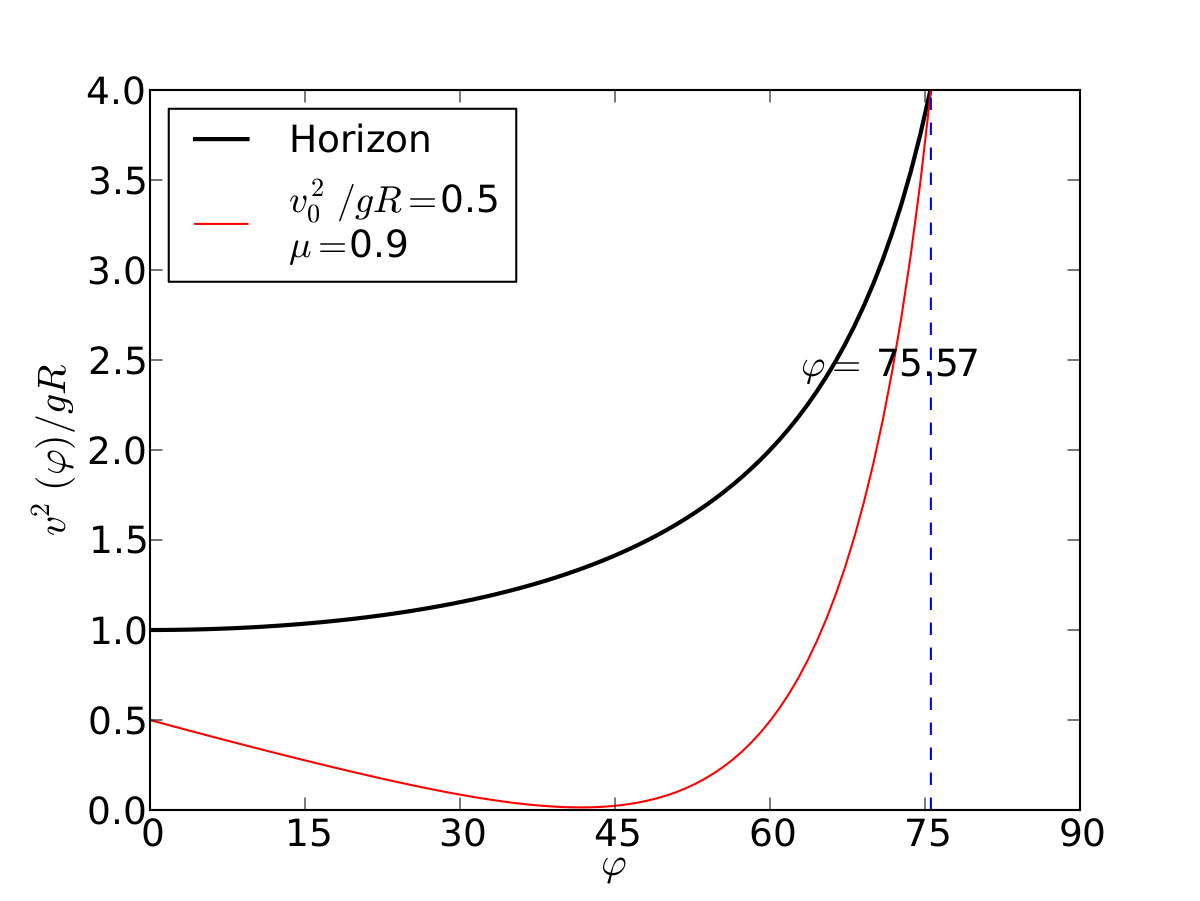
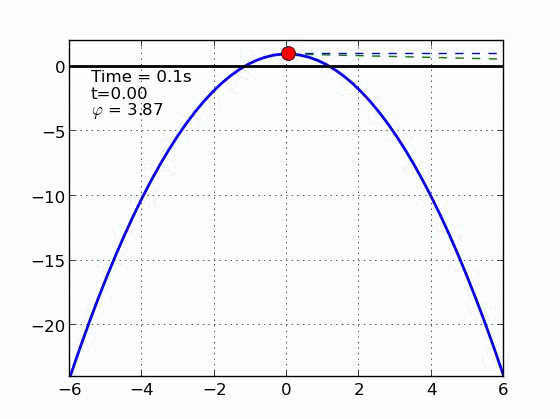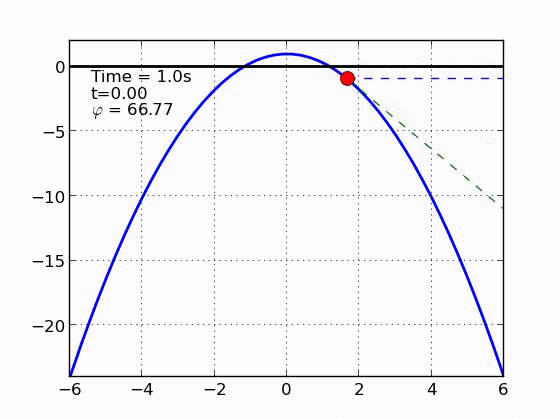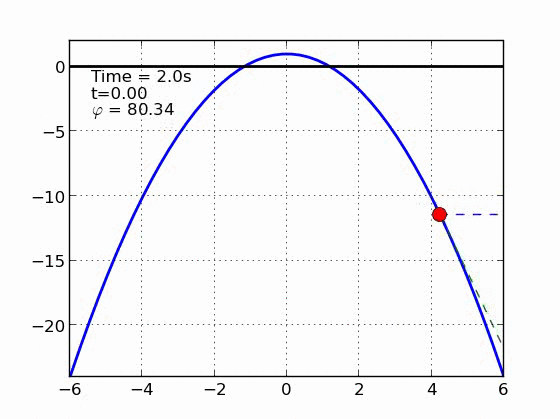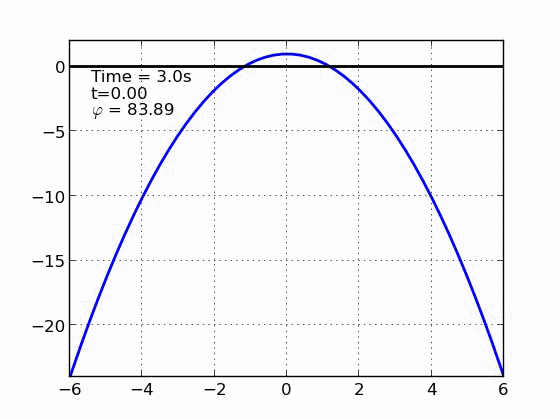
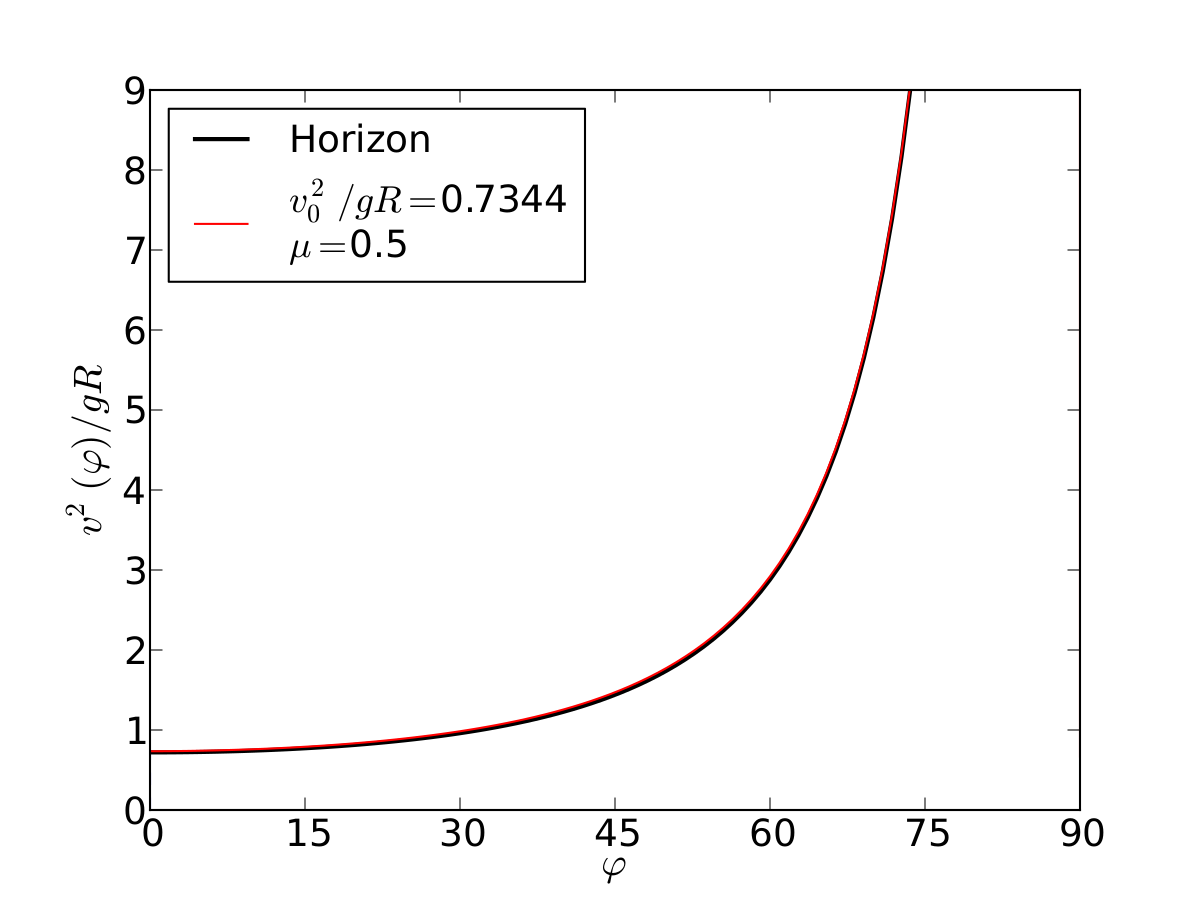
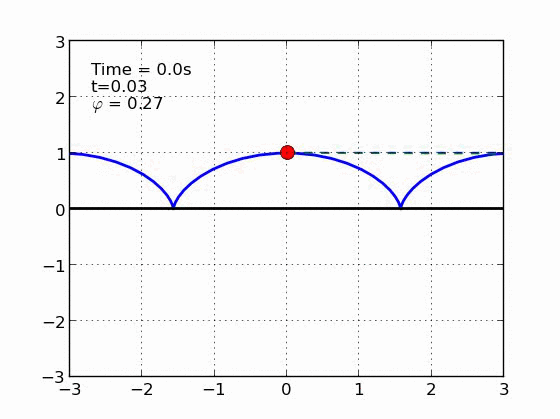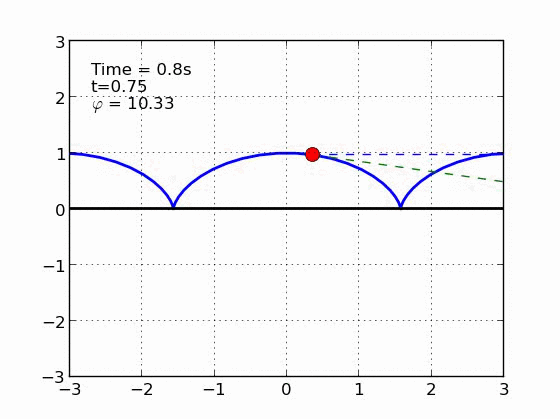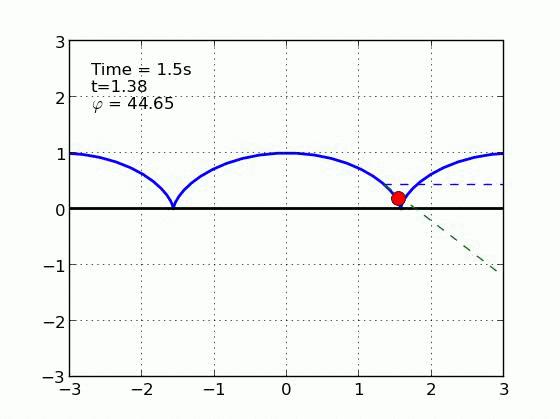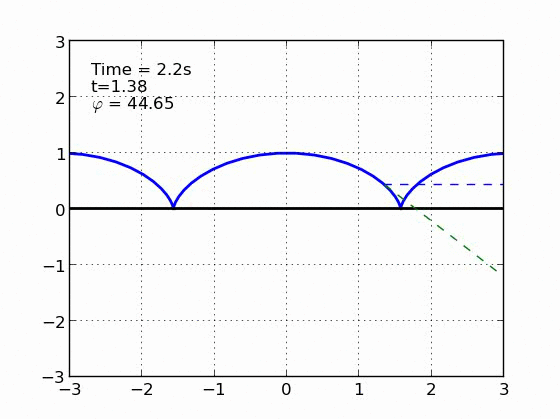
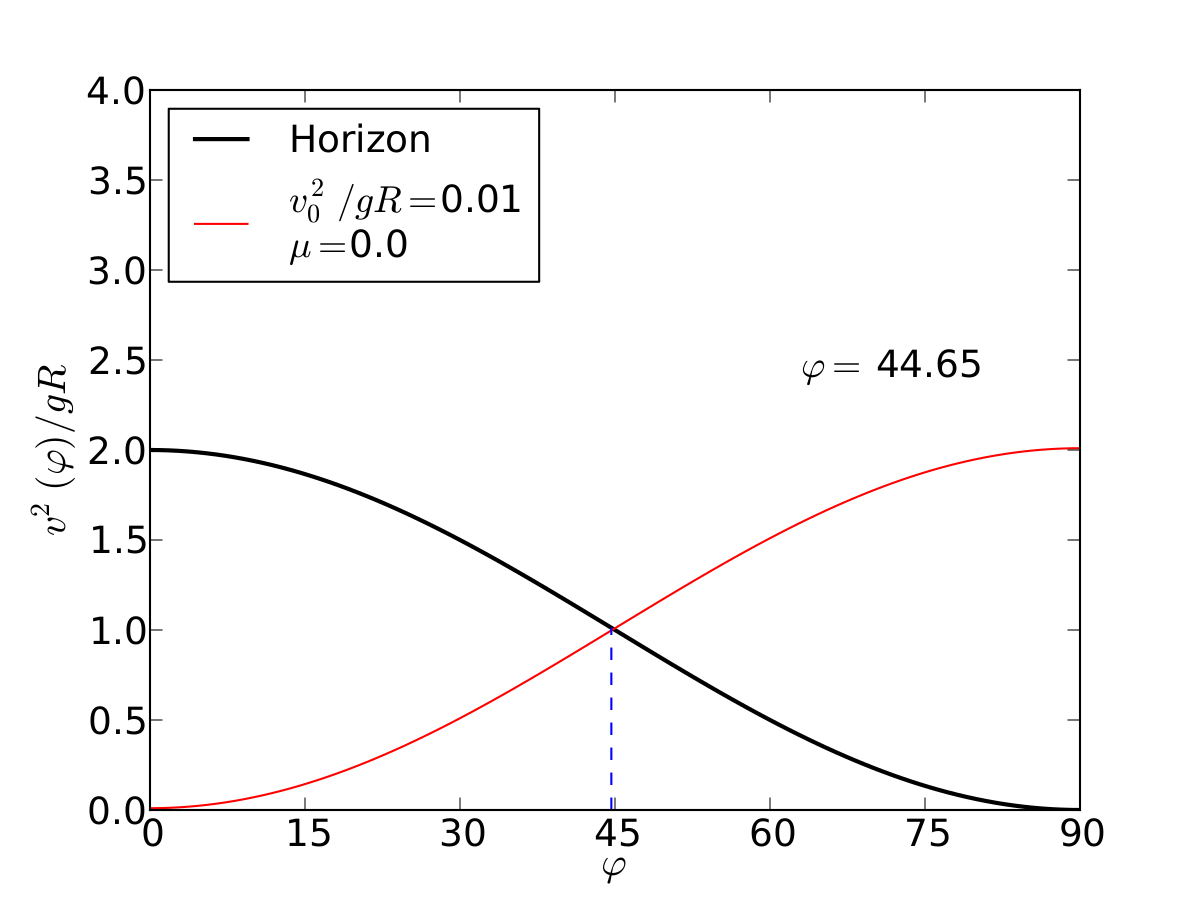
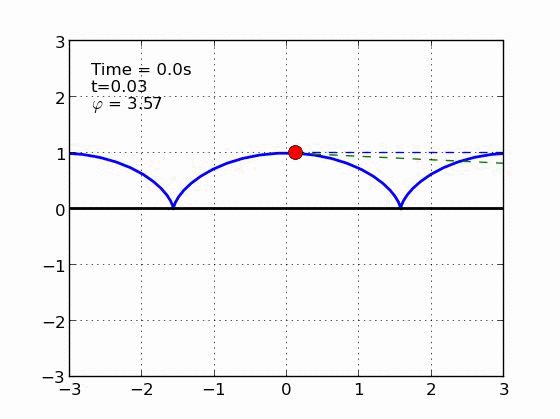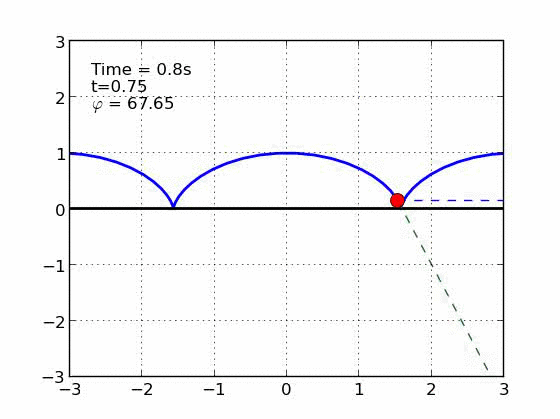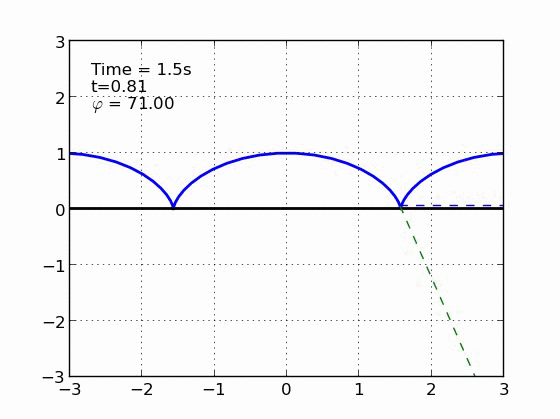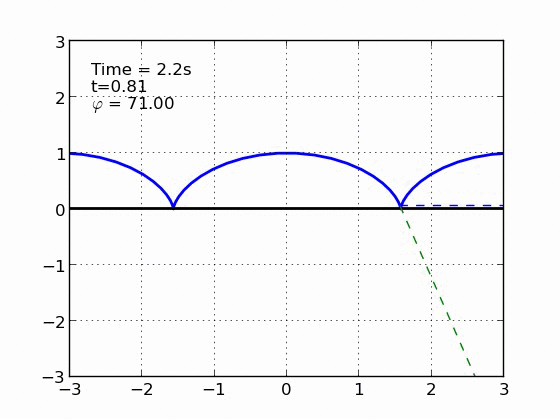
Un esquiador (una partícula) que se desliza sobre una superficie circular se despega de ella cuando la fuerza normal es cero. Encontrar el ángulo de despegue es un problema típico de mecánica elemental. Nosotros incluímos fricción y además generalizamos a superficies arbitrarias.
FUENTES
 Sliding down an arbitrary curve in the presence of friction,
Sliding down an arbitrary curve in the presence of friction,F. González-Cataldo, Gonzalo Gutiérrez and Julio Yáñez.
American Journal of Physics 85, 108 (2017). Available on the arXiv.
EJEMPLOS
|
Circulo | |
|---|---|
|
| |
|
| |
|
| |
|
| |
|
| |
|
Elipse | |
|
| |
|
| |
|
| |
|
Catenaria | |
|
| |
|
| |
|
| |
|
Parábola | |
|
| |
|
| |
|
| |
|
| |
|
Cicloide | |
|
| |
|
| |
|
| |
Código (python)
#* SLIDING DOWN AN ARBITRARY CURVE *#
#* IN THE PRESENCE OF FRICTION *#
#* *#
#* This program animates a particle sliding on a curved *#
#* surface with a friction coefficient mu. *#
#* More information in: *#
#* F. González-Cataldo et al. Am. J. of Phys. 85, 108 (2017). *#
#* and https://arxiv.org/abs/1512.00515. *#
#****************************************************************#
# AUTHOR: FELIPE GONZALEZ CATALDO, July 2015.
#!/usr/bin/python
from numpy import *
from pylab import *
import scipy.integrate as integrate
from scipy.integrate import quad
import matplotlib.animation as animation
g = 9.8 # acceleration due to gravity, in m/s^2
R = 1.0 # length of pendulum 1 in m
dt = 0.02
tmax = 0.8
xmin, xmax = -5*R, 5*R
ymin, ymax = -5*R, 2*R
# th0 initial angle
case = 'circle'
gamma=1.0
th0 = 0.0
vo2 = 0.09*g*R
mu = 0.1
alphas = linspace(0,2*pi,100)
if case=='circle':
tmax = 1.5
xmin, xmax = -2*R, 2*R
ymin, ymax = -2*R, 2*R
alphas = linspace(0,2*pi,100)
elif case=='ellipse':
tmax = 2.0
gamma=0.3
L = 2*R if gamma<1 else 2.0*gamma*R
xmin, xmax = -L, L
ymin, ymax = -L, L
alphas = linspace(0,2*pi,100)
elif case=='parabola':
tmax = 3.0
gamma=1.2
L = 5*R*gamma
xmin, xmax = -L, L
ymin, ymax = -4*L, 2*R
alphas = linspace(-10,10,100)
elif case=='catenary':
tmax = 3.0
L = 4*R
xmin, xmax = -L, L
ymin, ymax = -4*L, L
alphas = linspace(-5,5,100)
elif case=='cycloid':
tmax = 2.2
L = 3*R
xmin, xmax = -L, L
ymin, ymax = -L, L
alphas = linspace(-4*pi,4*pi,100)
########### PARTICLE POSITION PARAMETRIZATION #############
def r(alpha):
if case=='circle':
return R*sin(alpha), R*cos(alpha)
elif case=='ellipse':
return R*gamma*sin(alpha), R*cos(alpha)
elif case=='parabola':
return R*gamma*alpha, R*(1-alpha**2)
elif case=='catenary':
return R*alpha, R*(2.0-cosh(alpha))
elif case=='cycloid':
return 0.5*R*(alpha+sin(alpha)), 0.5*R*(1.0+cos(alpha))
def alpha(phi):
if case=='circle':
return phi
elif case=='ellipse':
return arctan(gamma*tan(phi))
elif case=='parabola':
return 0.5*gamma*tan(phi)
elif case=='catenary':
return arcsinh(tan(phi))
elif case=='cycloid':
return 2*phi
def drdp(phi): # dr/dphi = r'(phi)
drda = 0.0
drdp = 0.0
if case=='circle':
drda = R
dadp = 1.0
elif case=='ellipse':
drda = sqrt( (R*gamma*cos(alpha(phi)))**2 + (R*sin(alpha(phi)))**2 )
dadp = gamma/(cos(phi)**2+gamma**2*sin(phi)**2)
elif case=='parabola':
drda = sqrt( gamma**2 + 4*alpha(phi)**2 )
dadp = 0.5*gamma/cos(phi)**2
elif case=='catenary':
drda = R*cosh(alpha(phi))
dadp = 1.0/cos(phi)
elif case=='cycloid':
drda = R*cos(0.5*alpha(phi))
dadp = 2.0
return drda*dadp
def horizon(phi):
if case=='circle':
return cos(phi)
elif case=='ellipse':
return gamma**2*cos(phi)/(gamma**2*sin(phi)**2+cos(phi)**2)**1.5
elif case=='parabola':
return 0.5*gamma**2/cos(phi)**2
elif case=='catenary':
return 1.0/cos(phi)
elif case=='cycloid':
return 2.0*cos(phi)**2
############### CALCULATE THE VELOCITY ##################
def kappa(phi):
if case=='circle':
return 1.0/R
elif case=='ellipse':
return (gamma**2*sin(phi)**2+cos(phi)**2)**1.5/(gamma**2*R)
elif case=='parabola':
return 2*cos(phi)**3/(gamma**2*R)
elif case=='catenary':
return cos(phi)**2/R
elif case=='cycloid':
return 1.0/(2*R*cos(phi))
def integrand(phi, mu):
return (sin(phi)-mu*cos(phi))*exp(-2*mu*phi)/(R*kappa(phi))
def integral(phi,mu):
return quad(integrand, 0, phi, args=(mu))[0]
def velocity2(phi,mu,vo2):
return g*R*exp(2*mu*phi)*(vo2/(g*R)+2*integral(phi,mu))
#########################################################
############## SOLVE DIFF. EQUATIONS #####################
def IntegrateODE(state, t):
# state = ( phi )
dydx = zeros_like(state) # dydx = dy/dx = function derivatives
# dydx[0] = sqrt(velocity2(state[0],mu,vo2))/drdp(state[0]) # dy/dx = dphi/dt = v(phi)/|dr/dphi|
# SINCE dphi/dt = v(phi)/|dr/dphi| < sqrt(gRH)/|dr/dphi|, the right-hand side limits the values of interest
vel = velocity2(state[0],mu,vo2) if velocity2(state[0],mu,vo2)>0.0 else 0.0
value = sqrt(vel)/drdp(state[0]) # dy/dx = dphi/dt = v(phi)/|dr/dphi|
dydx[0] = value if value<=sqrt(g*R*horizon(state[0]))/drdp(state[0]) else 0.0
return dydx
# create a time array from 0..100 sampled at 0.05 second steps
t = arange(0.0, tmax, dt)
# initial state
state = array([th0])
# integrate your ODE using scipy.integrate.
y = integrate.odeint(IntegrateODE, state, t)
#########################################################
############## PARAMETRIZE TRAJECTORY ####################
pf = 0
t0 = 0
step = 0
x1 = []
y1 = []
for i in xrange(len(t)):
p = y[:,0][i] if i<len(y[:,0]) and y[:,0][i]<=0.5*pi else 0.999*pi/2
if velocity2(p,mu,vo2)/(g*R) <= horizon(p) and step==0:
x1 += [ r(alpha(p))[0] ] #[R*gamma*sin(alpha(p))]
y1 += [ r(alpha(p))[1] ] #[R*cos(alpha(p))]
t0 = t[i]
# print "Primer caso: velocity2(p,mu,vo2)/(g*R)=",velocity2(p,mu,vo2)/(g*R),"menor que",horizon(p),"para i=",i,"y=phi(t)=",p*180/pi
elif velocity2(p,mu,vo2)/(g*R) > horizon(p):
if step==0:
step = i
pf = 0.5*(y[:,0][i] + y[:,0][i-1])
x1 += [ r(alpha(pf))[0] + sqrt(velocity2(pf,mu,vo2))*cos(pf)*(t[i]-t0) ]
y1 += [ r(alpha(pf))[1] - sqrt(velocity2(pf,mu,vo2))*sin(pf)*(t[i]-t0) - 0.5*g*(t[i]-t0)**2 ]
#print "Supero horizonte: velocity2(p,mu,vo2)/(g*R)=",velocity2(p,mu,vo2)/(g*R),"mayor que",horizon(p),"para i=",i,"y=phi(t)=",p*180/pi
elif velocity2(p,mu,vo2)<=0: # If the particle gets stuck
x1 += [ r(alpha(pf))[0] ] #[R*gamma*sin(alpha(pf))]
y1 += [ r(alpha(pf))[1] ] # [R*cos(alpha(pf))]
else:
print "No se cumple ni una en i=",i,"t[i]=",t[i],"phi[i]=",y[i]*180/pi
print "Porque velocity2(p,mu,vo2)/(g*R)=",velocity2(p,mu,vo2)/(g*R),"no es menor que",horizon(p),"y=phi(t)=",p*180/pi
x1 = array(x1)
y1 = array(y1)
#########################################################
############## DRAW SURFACE ####################
fig = plt.figure()#figsize=(0.7*8,0.7*6))
params = {'legend.fontsize':18, 'text.fontsize':28,'xtick.labelsize':18, 'ytick.labelsize':18, 'xtick.labelsize':18, 'axes.labelsize':19,'xtick.major.size':6,'ytick.major.size':6}
rcParams.update(params)
ax = fig.add_subplot(111, autoscale_on=False, xlim=(xmin, xmax), ylim=(ymin, ymax), aspect='auto')
ax.grid(lw=1)
x_s = r(alphas)[0] #R*gamma*sin(phi)
y_s = r(alphas)[1] #R*cos(phi)
surface, = ax.plot( x_s, y_s, '-', lw=3)
floor, = ax.plot( linspace(xmin,xmax,100), [0.0]*100, '-k', lw=2)
line1, = ax.plot([],[], '--b', lw=1)
line2, = ax.plot([],[], '--g', lw=1)
mass, = ax.plot([],[], 'ro', ms=15)
#########################################################
################# ANIMATION ############################
time_text = ax.text(0.05, 0.88, '', transform=ax.transAxes,fontsize=18)
t_text = ax.text(0.05, 0.83, '', transform=ax.transAxes,fontsize=18)
phi_text = ax.text(0.05, 0.78, '', transform=ax.transAxes,fontsize=18)
def init():
line1.set_data([], [])
line2.set_data([], [])
mass.set_data([], [])
time_text.set_text('')
phi_text.set_text('')
t_text.set_text('')
return mass, line1, line2, time_text, phi_text, t_text
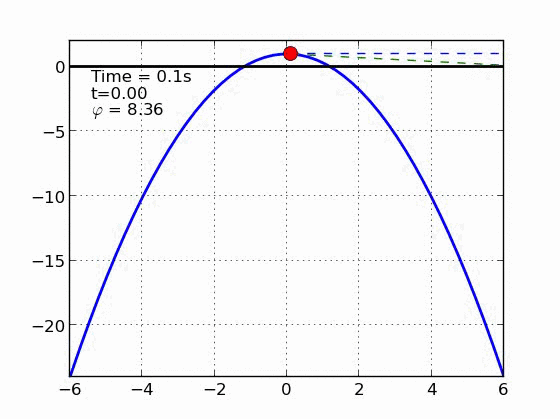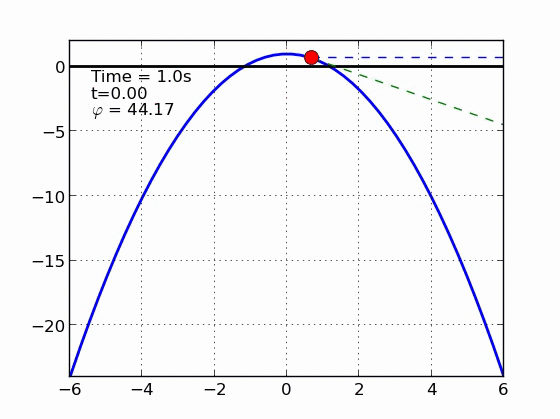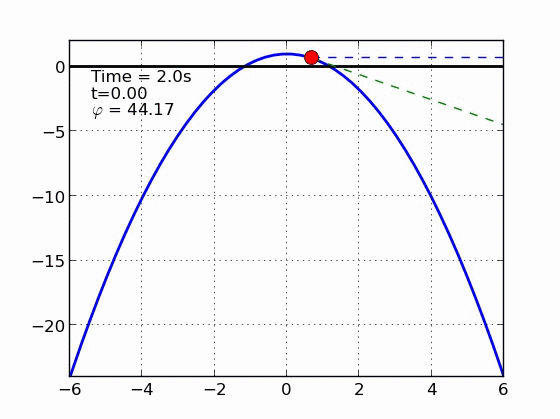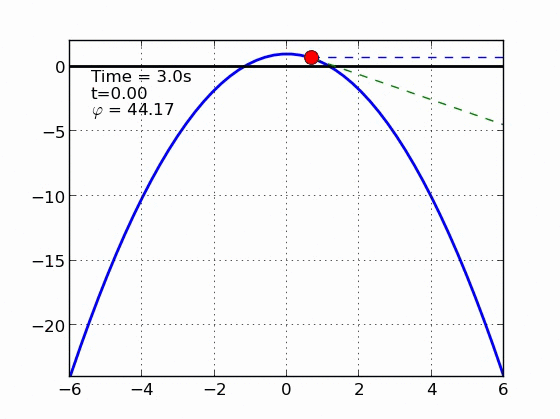
def animate(i):
line1x = [(x1[i],xmax) if i<step or step==0 else (x1[step],xmax) ]
line1y = [(y1[i],y1[i]) if i<step or step==0 else (y1[step],y1[step])]
line2x = [(x1[i],x1[i]+2*xmax*cos(y[:,0][i])) if i<step or step==0 else (x1[step],x1[step]+2*xmax*cos(y[:,0][step]))]
line2y = [(y1[i],y1[i]-2*xmax*sin(y[:,0][i])) if i<step or step==0 else (y1[step],y1[step]-2*xmax*sin(y[:,0][step]))]
line1.set_data(line1x, line1y)
line2.set_data(line2x, line2y)
mass.set_data(x1[i], y1[i])
# TEXT
my_t = i*dt if i<step else step*dt
text_phi = (y[:,0][i]*180/pi) if i<step or step==0 else (pf*180/pi)
time_text.set_text('Time = %.1fs'%(i*dt))
t_text.set_text('t=%.2f'%my_t)
phi_text.set_text(r'$\varphi$ = %.2f'%text_phi)
return mass, line1, line2, time_text, phi_text, t_text
axis('equal')
#ani = animation.FuncAnimation(fig, animate, arange(1, len(t)), interval=50, blit=True, init_func=init)#,repeat_delay=1000)
ani = animation.FuncAnimation(fig, animate, arange(1, len(t)), interval=50, blit=False, init_func=init)#,repeat_delay=1000)
# t_video = Nframes/fps = len(t)/fps
# fps <= Nframes/2 ( or you get bad quality, due to interpolation)
#ani.save('ejemplo.mp4', fps=0.4*len(t)/2) # Video lasts t_video = len(t)/fps = len(t)/(0.4*len(t)/2) = 2/0.4 = 5 sec
fig = plt.figure(2)
params = {'legend.fontsize':18, 'text.fontsize':18,'xtick.labelsize':18, 'ytick.labelsize':18, 'xtick.labelsize':18, 'axes.labelsize':19,'xtick.major.size':6,'ytick.major.size':6}
rcParams.update(params)
ax = fig.add_subplot(111)
mgr = get_current_fig_manager()
#mgr.window.wm_geometry("+600+55")
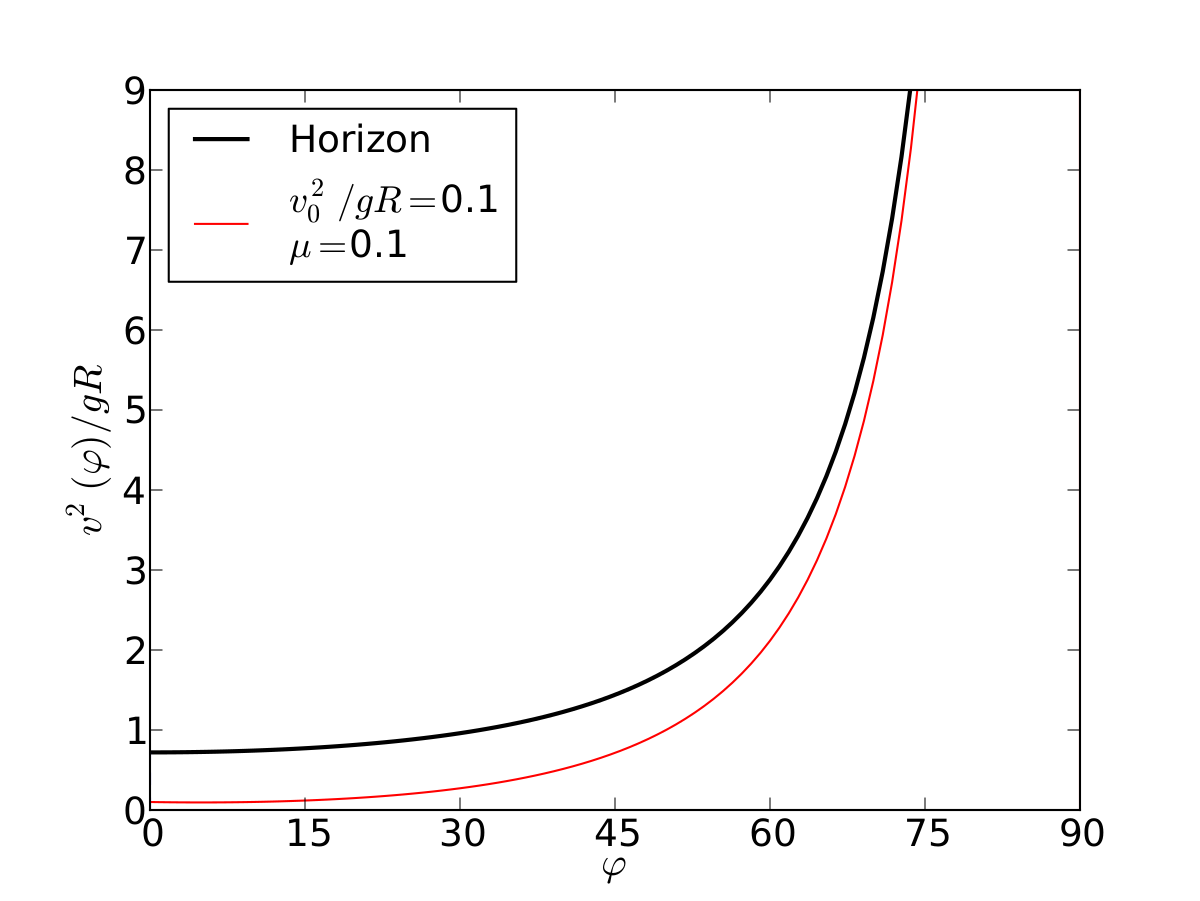
ymax = horizon(0)
if horizon(0)<1:
ymax = 1.0
elif horizon(0)>4:
ymax = 9.0
xlim(0,0.5*pi)
ylim(0,ymax)
xlabel(r'$\varphi$')
ylabel(r'$v^2(\varphi)/gR$')
xticks( [0,pi/12,2*pi/12,3*pi/12,4*pi/12,5*pi/12,6*pi/12], [0,15,30,45,60,75,90] )
phis = [p for p in linspace(0,0.5*pi,100)]
vels = [velocity2(p,mu,vo2)/(g*R) for p in phis ]
j=0
for i in xrange(len(vels)):
if vels[i]<0: j=i
if j>0: vels[i]=0.0
horz = [horizon(p) for p in phis]
dashed = linspace(0,horizon(pf))
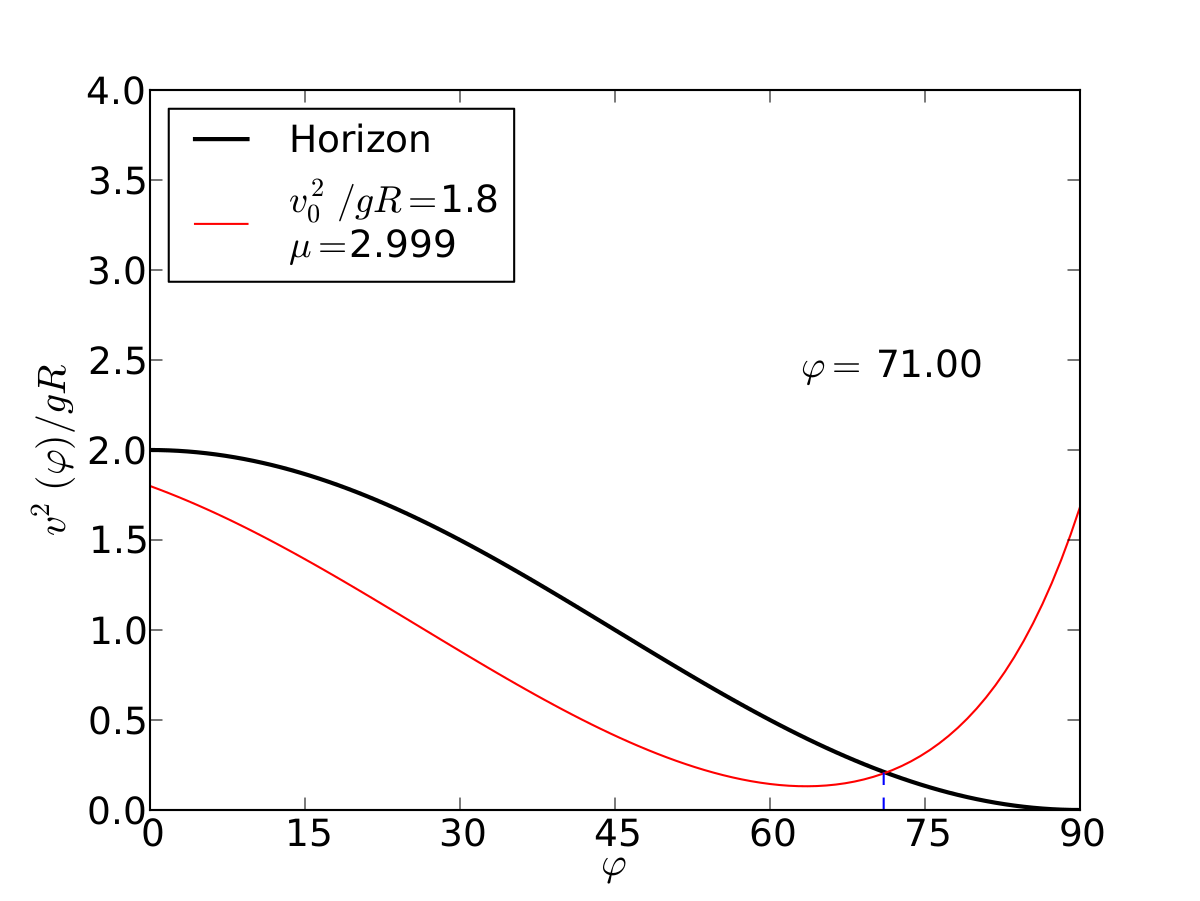
ax.plot(phis , horz, '-k', lw=2,label='Horizon')
ax.plot(phis , vels, '-r',label=r'$v_0^2/gR=$'+str(vo2/(g*R))+'\n$\mu=$'+str(mu))
ax.plot( [ pf ]*len(dashed) , dashed , '--')
text= ax.text(0.7, 0.6, r'$\varphi=$ %.2f'%(pf*180/pi), transform=ax.transAxes, fontsize=18)
legend(loc=1)
#savefig('ejemplo.pdf')
plt.show()
Ejecutando el programa
Para ejecutar el programa, guarde el código anterior como "sliding-with-friction.py", y ejecute
Esto generará la animación. Si deseas guardar la animacion, quita el comentario '#' en la linea