Programas

Modelo De Ising

« Programas

El modelo de Ising es un modelo matemático simple que permite estudiar un sistema de spines (o dipolos magneticos) interactuantes. El modelo en 2 dimensiones da cuenta de un cambio de fase a baja temperatura, en la cual el sistema se magnetiza. El Hamiltoniano que describe el sistema es

\displaystyle H = -\sum_{ij} J_{ij}\ S_i S_j -\mu \sum_j h_j S_j

La interacción spin-spin se clasifica de la siguiente manera:

  • J_{ij}>0: ferromagnética
  • J_{ij}<0: antiferromagnética
  • J_{ij}=0: no interactuante

De acuerdo a la solución analítica, encontrada por Lars Onsager, la transición ocurre a una temperatura crítica

\displaystyle T_c=\frac{2J}{k\ln(1+\sqrt{2})} \approx 2.2691853\, \frac{J}{k_B}.

para el caso isotrópico (J_{ij}=J). La magnetización promedio está dada, en la solución de Onsager, por

\displaystyle \left.M=\left(1-\left[\sinh\left(\ln\left(1+\sqrt{2}\right)\frac{T_c}{T}\right)\right]^{-4}\right)\right.^{\frac{1}{8}}.

EJEMPLOS

Sin campo magnético externo

La versión más simple del modelo de Ising considera interacción únicamente a primeros vecinos, sin la presencia den un campo magnético externo. El Hamiltoniano en este caso es

\displaystyle H = -J\sum_{ij} S_i S_j,

donde J=J_{ij} toma el mismo valor para todos los pares de spines.

  • J=1, kT=1.2J

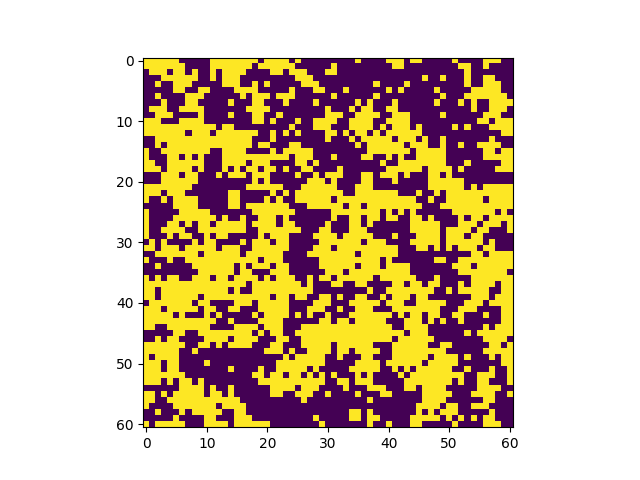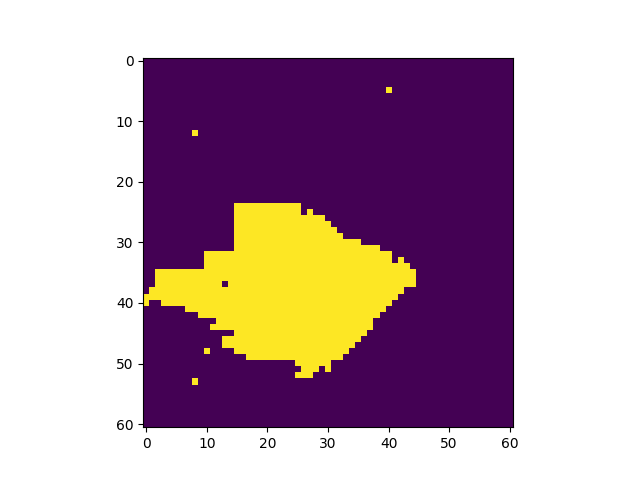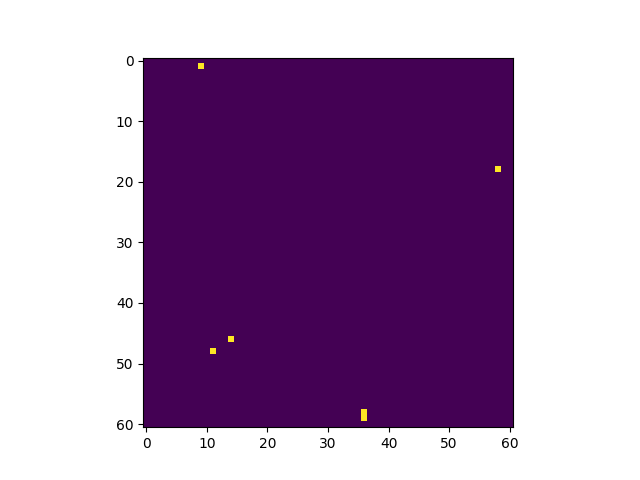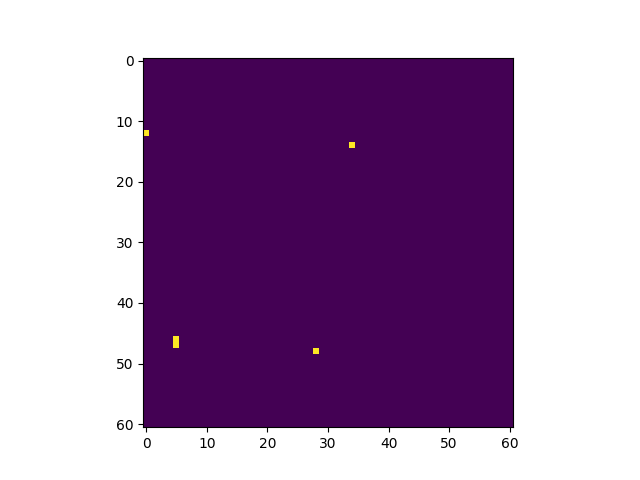
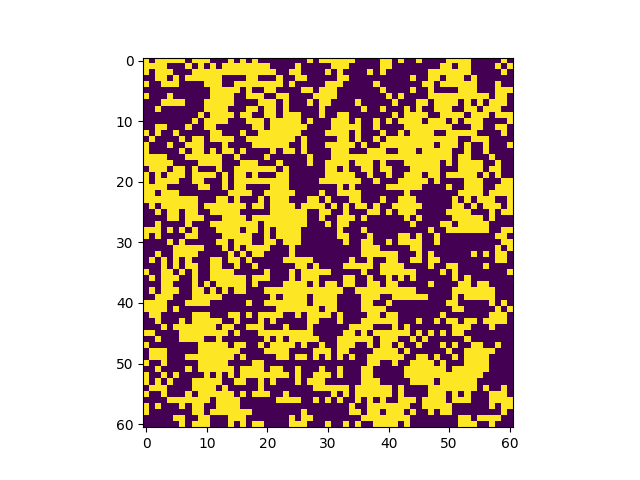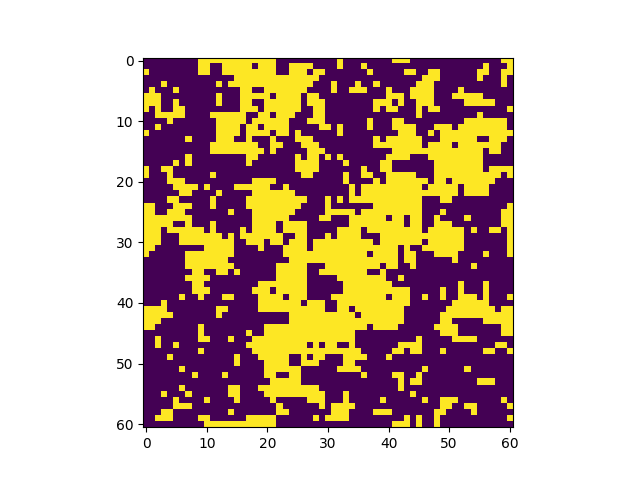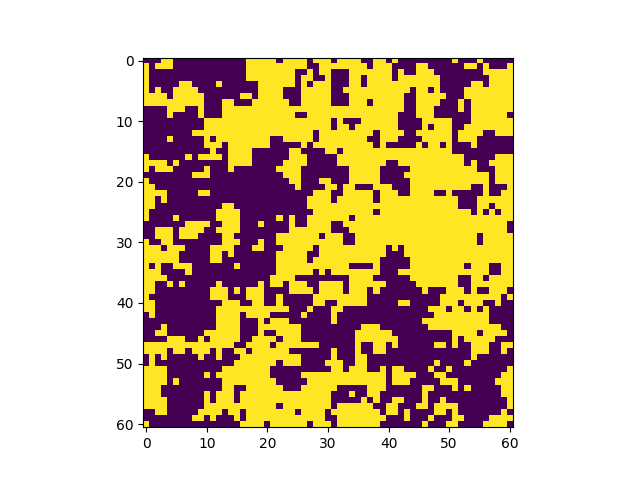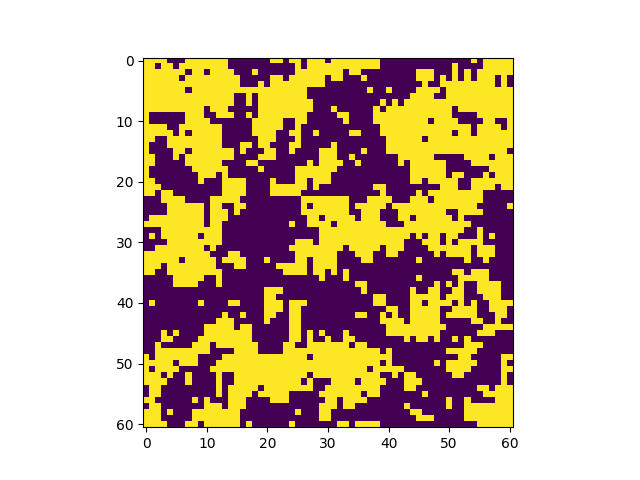
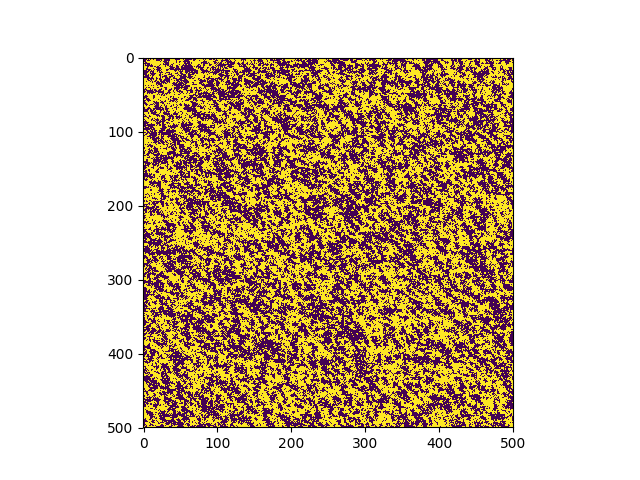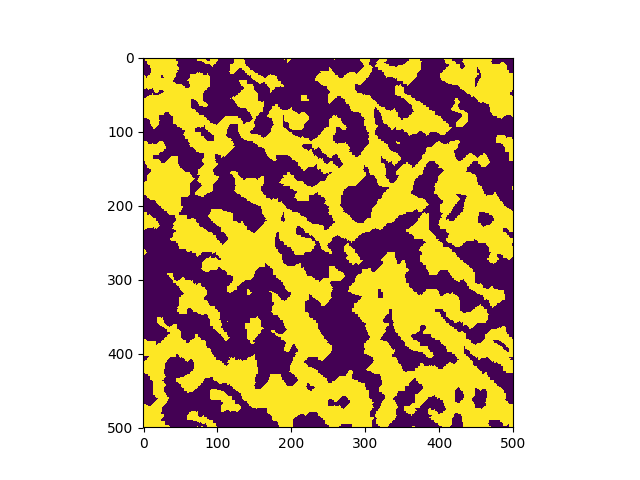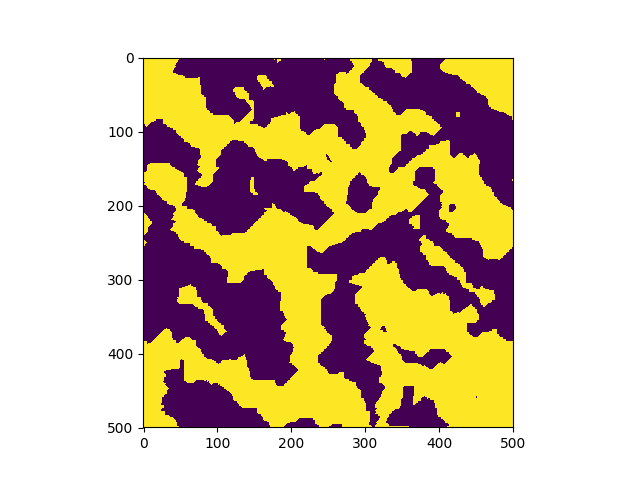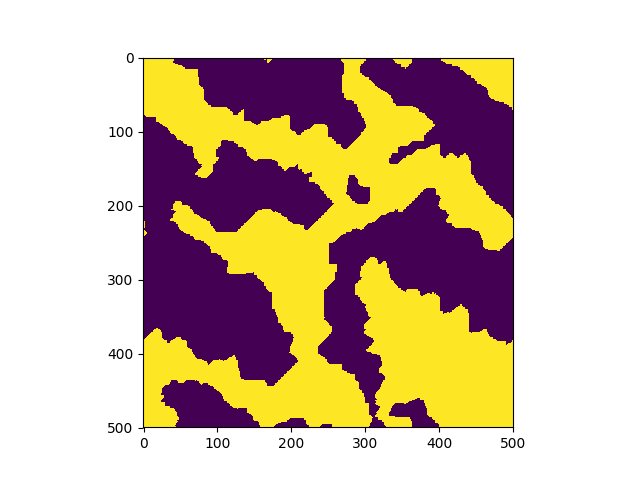
El sistema se inicializa en una configuracion aleatoria de +1 y (-1) y evoluciona de acuerdo al algoritmo de Metropolis-Hasting. En tan sólo unos pocos pasos, el sistema se magnetiza.

  • J=1, kT=2.5J

La temperatura es mayor a la temperatura crítica. No hay transición de fase, el sistema no se magnetiza.

  • J=1, kT=0.1J

Transición de fase en un sistema más grande (500x500).

Código (python)

#!/usr/local/bin/python
#***********************************************************************#
#*                      THE ISING MODEL                                *#
#*                                                                     *#
#* This program uses the Metropolis Monte Carlo algorithm              *#
#* to simulate the Ising model, with Hamiltonian                       *#
#*                         ----                                        *#
#*                    H =   \    -J_ij * Si*Sj                         *#
#*                          /                                          *#
#*                         ----ij                                      *#
#*                                                                     *#
#* Adapted from B. Militzer course, EPS109, UC Berkeley, 2018.        *#
#***********************************************************************#
 # AUTHOR: FELIPE GONZALEZ CATALDO, September 2018.
from pylab import *

fig = figure(1)
ax = subplot(111)

# Jij = J for all i,j:  Coupling constant (Jij>0: ferromagnetic, Jij<0: antiferromagnetic, Jij=0: non magnetic )
J= 1                   # In eV, ferromagnetic
kT = 1.2*J             # In eV

# ONSAGER SOLUTION FOR 2D LATTICE: kT = 2*J/(ln(1+sqrt(2))) = 2.2691853

n=61
mat = random(size=(n,n))   # Matrix of randoms in the interval  [ 0.0 1.0 ]
mat = 2*floor(2*mat)-1     # Martrix of random 1's and -1's

img = imshow(mat)
show(block=False)

nBlocks = 100
for iBlock in xrange(nBlocks):

 for ix in xrange(n):
  ixp = (ix+1) % n      # Neighbor to the right
  ixm = (ix-1) % n      # Neighbor to the left
  for iy in xrange(n):
   iyp = (iy+1) % n     # Neighbor above
   iym = (iy-1) % n     # Neighbor below
   s = mat[ixm,iy] + mat[ixp,iy] + mat[ix,iyp] +  mat[ix,iym]  # Sum of neighbors spins
   mOld = mat[ix,iy]   # Old value of the spin
   EOld = -J*mOld*s     # Si * (S_above + S_below + S_left + S_right)
   mNew = -mOld
   ENew = -J*mNew*s     # sum_ij  Si'*Sj, where Si' = -Si
   Ediff = ENew - EOld     # No need to sum over all the lattice, just this  (ix,iy)  site energy.

   prob = exp(-Ediff/kT)
   if ENew < EOld:
    mat[ix,iy] = mNew
   else:
    mat[ix,iy] = mNew if random() < exp(-Ediff/kT) else mOld

 #print iBlock
 img.set_data(mat)
 plt.pause(1e-30)
 draw()

 #savefig('is'+str(iBlock)+'.png')
 
[$[Get Code]]