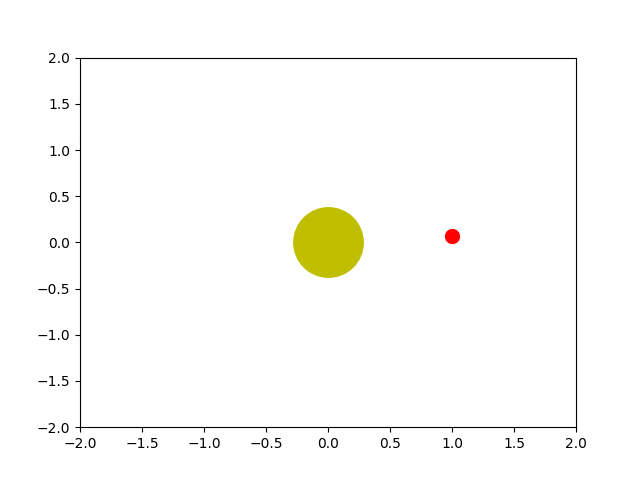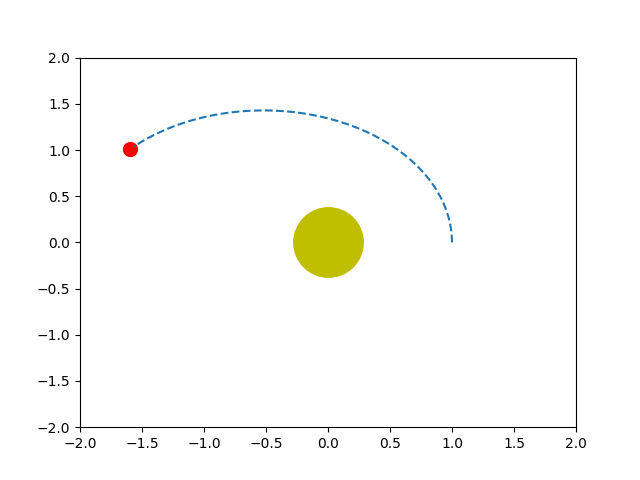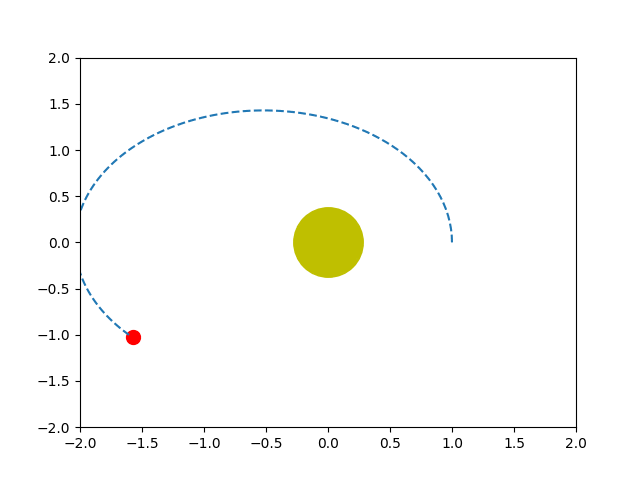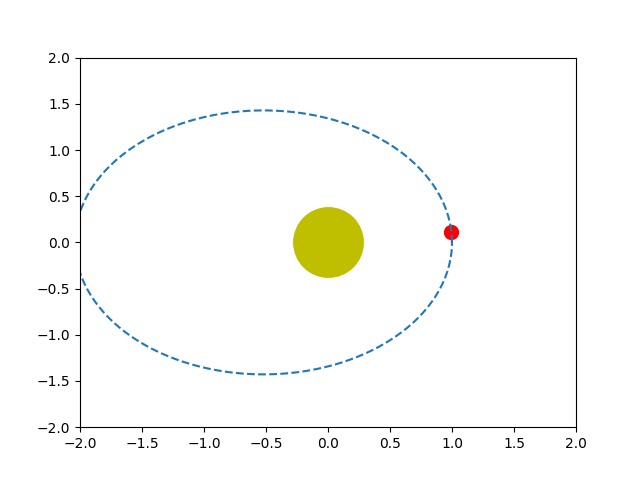
Programas

Kepler Orbits

« Programs

A planet of mass m around the sun follows the orbit dictated by Newton's law of gravity

\displaystyle \vec F = - \frac{GMm}{r^2}\hat r.

Since \vec F=m \vec r''(t), we obtain the differential equation

\displaystyle \vec r''(t) = - \frac{GM}{r^2}\hat r= - \frac{GM}{r^3}\vec r.

In cartesian coordinates, \vec r(t)=(x(t),y(t)), and the equation above gives rise to two second-order differential equations:

\displaystyle x''(t) = - \frac{GM}{(x(t)^2+y(t)^2)^{3/2}}x(t),\qquad \displaystyle y''(t) = - \frac{GM}{(x(t)^2+y(t)^2)^{3/2}}y(t).

Using the notation x_1(t)\equiv x(t), y_1(t)\equiv y(t), x_2(t)\equiv x'(t), y_2(t)\equiv y'(t), we can split the equations above into four first-order, coupled differential equations:

\displaystyle x_1'(t) = x_2, <br />y_1'(t) = y_2, <br />x_2'(t) = - \frac{GM}{({x_1}^2+{y_1}^2)^{3/2}}\quad x_1, <br />y_2'(t) = - \frac{GM}{({x_1}^2+{y_1}^2)^{3/2}}\quad y_1,


INDEX

Code (C++)

//
// This program solves the differential equation
//             m R''(t) = - GMm/r² r^
// where R=(x,y) and r^ = (x,y)/sqrt(x²+y²)
// using Runge-Kutta methods.

#include<iostream>
#include<fstream>
#include<cmath>
using namespace std;

const double G=0.00011859645; // in AU³/(earthmass*year²)
const double m=1;             // earthmass
const double M=332946.05;     // sunmass=332946.05 earthmass
const double tau=0.01, tmax=5; // year

typedef struct vect{
 double x, y, z;
} Vector;


// We separate the 2nd order vector equation in 4 first-order differential equations:
// x1(t) = x(t)
// y1(t) = y(t)
// x2(t) = x'(t)
// y2(t) = y'(t)

double fx1(double  x1, double x2, double y1, double y2, double t){ return x2; } // x1'(t) = x2(t) = fx1(x1,x2,y1,y2,t)
double fy1(double  x1, double x2, double y1, double y2, double t){ return y2; } // y1'(t) = y2(t) = fx2(x1,x2,y1,y2,t)
double fx2(double  x1, double x2, double y1, double y2, double t)
{
 return -G*M*x1/pow(x1*x1+y1*y1,1.5); // x2'(t) = -G*M*x1/R³ = fy1(x1,x2,y1,y2,t)
}
double fy2(double  x1, double x2, double y1, double y2, double t)
{
 return -G*M*y1/pow(x1*x1+y1*y1,1.5); // y2'(t) = -G*M*y1/R³ = fy1(x1,x2,y1,y2,t)
}

Vector RungeLenz(double x, double y, double vx, double vy)
{
 double r=sqrt(x*x+y*y);
 double px=m*vx, py=m*vy;
 double Lz=x*py-y*px;
 Vector A;
 A.x =  Lz*py-m*(G*M*m)*x/r;
 A.y = -Lz*px-m*(G*M*m)*y/r;
 return A;
}

///////////////////////////////
// METHODS                   //
///////////////////////////////

// Runge-Kutta first order
void RK1(double &x1, double &x2, double &y1, double &y2, double &t)
{
 double k1x1, k1x2, k1y1, k1y2;

 k1x1 = tau*fx1(x1,x2,y1,y2,t);
 k1x2 = tau*fx2(x1,x2,y1,y2,t);
 k1y1 = tau*fy1(x1,x2,y1,y2,t);
 k1y2 = tau*fy2(x1,x2,y1,y2,t);

 x1 = x1 + k1x1;
 x2 = x2 + k1x2;
 y1 = y1 + k1y1;
 y2 = y2 + k1y2;
}

// Runge-Kutta de second order
void RK2(double &x1, double &x2, double &y1, double &y2, double &t)
{
 double k1x1, k1x2, k1y1, k1y2;
 double k2x1, k2x2, k2y1, k2y2;

 k1x1 = tau*fx1(x1,x2,y1,y2,t);
 k1x2 = tau*fx2(x1,x2,y1,y2,t);
 k1y1 = tau*fy1(x1,x2,y1,y2,t);
 k1y2 = tau*fy2(x1,x2,y1,y2,t);

 k2x1 = tau*fx1(x1+k1x1,x2+k1x2,y1+k1y1,y2+k1y2,t);
 k2x2 = tau*fx2(x1+k1x1,x2+k1x2,y1+k1y1,y2+k1y2,t);
 k2y1 = tau*fy1(x1+k1x1,x2+k1x2,y1+k1y1,y2+k1y2,t);
 k2y2 = tau*fy2(x1+k1x1,x2+k1x2,y1+k1y1,y2+k1y2,t);

 x1 = x1 + 0.5*(k1x1+k2x1);
 x2 = x2 + 0.5*(k1x2+k2x2);
 y1 = y1 + 0.5*(k1y1+k2y1);
 y2 = y2 + 0.5*(k1y2+k2y2);
}

// Runge-Kutta third order
void RK3(double &x1, double &x2, double &y1, double &y2, double &t)
{
 double k1x1, k1x2, k1y1, k1y2;
 double k2x1, k2x2, k2y1, k2y2;
 double k3x1, k3x2, k3y1, k3y2;

 k1x1 = tau*fx1(x1,x2,y1,y2,t);
 k1x2 = tau*fx2(x1,x2,y1,y2,t);
 k1y1 = tau*fy1(x1,x2,y1,y2,t);
 k1y2 = tau*fy2(x1,x2,y1,y2,t);

 k2x1 = tau*fx1(x1+0.5*k1x1, x2+0.5*k1x2, y1+0.5*k1y1, y2+0.5*k1y2, t+0.5*tau);
 k2x2 = tau*fx2(x1+0.5*k1x1, x2+0.5*k1x2, y1+0.5*k1y1, y2+0.5*k1y2, t+0.5*tau);
 k2y1 = tau*fy1(x1+0.5*k1x1, x2+0.5*k1x2, y1+0.5*k1y1, y2+0.5*k1y2, t+0.5*tau);
 k2y2 = tau*fy2(x1+0.5*k1x1, x2+0.5*k1x2, y1+0.5*k1y1, y2+0.5*k1y2, t+0.5*tau);

 k3x1 = tau*fx1(x1-k1x1+2*k2x1, x2-k1x2+2*k2x2, y1-k1y1+2*k2y1, y2-k1y2+2*k2y2, t+tau);
 k3x2 = tau*fx2(x1-k1x1+2*k2x1, x2-k1x2+2*k2x2, y1-k1y1+2*k2y1, y2-k1y2+2*k2y2, t+tau);
 k3y1 = tau*fy1(x1-k1x1+2*k2x1, x2-k1x2+2*k2x2, y1-k1y1+2*k2y1, y2-k1y2+2*k2y2, t+tau);
 k3y2 = tau*fy2(x1-k1x1+2*k2x1, x2-k1x2+2*k2x2, y1-k1y1+2*k2y1, y2-k1y2+2*k2y2, t+tau);

 x1 = x1 +(k1x1+4*k2x1+k3x1)/6.0;
 x2 = x2 +(k1x2+4*k2x2+k3x2)/6.0;
 y1 = y1 +(k1y1+4*k2y1+k3y1)/6.0;
 y2 = y2 +(k1y2+4*k2y2+k3y2)/6.0;
}

double KineticEnergy(double x1, double x2, double y1, double y2, double t)
{
 return 0.5*m*(x2*x2+y2*y2);       // in earthmass*(AU/year)²
}

double PotentialEnergy(double x1, double x2, double y1, double y2, double t)
{
 return -G*M*m/sqrt(x1*x1+y1*y1);  // in earthmass*(AU/year)²
}


int main()
{
 double x1, x2, y1, y2, t; // x1= x, x2=vx, y1=y, y2=vy
 ofstream archivo("sol-tierraRK1.dat");
 for(x1=5, x2=0, y1=0, y2=5, t=0; t<tmax; t+=tau)
 {
  archivo << t << " " << x1 << " " << x2 << " " << y1 << " " << y2 << endl;
  RK1(x1,x2,y1,y2,t);
 }
 archivo.close();

 ofstream archivo2("sol-tierraRK2.dat");
 for(x1=5, x2=0, y1=0, y2=5, t=0; t<tmax; t+=tau)
 {
  archivo2 << t << " " << x1 << " " << x2 << " " << y1 << " " << y2 << endl;
  RK2(x1,x2,y1,y2,t);
 }
 archivo2.close();

 ofstream archivo3("sol-tierraRK3.dat");
 ofstream prop("props.dat");
//cout << "set terminal " << endl; //wxt size 600,600" << endl; // FIX WINDOW SIZE FOR GNUPLOT
 double A1, A2;
 for(x1=1, x2=0, y1=0, y2=7.28, t=0; t<tmax; t+=tau)
 {
  archivo3 << t << " " << x1 << " " << x2 << " " << y1 << " " << y2 << endl;
  A1 = RungeLenz(x1,y1,x2,y2).x;
  A2 = RungeLenz(x1,y1,x2,y2).y;
  prop << t << " " << KineticEnergy(x1,x2,y1,y2,t) << " " << PotentialEnergy(x1,x2,y1,y2,t)  << " " << A1 << " " << A2 << endl;

 // cout<<"plot [-2:2][-2:2] sqrt(1-x**2)  lc 1 t 'Circulo', -sqrt(1-x**2) lc 1 notitle, '-' ls 7 lc 6 ps 8 t 'Sol', '-' ls 7 lc 3 ps 2 t 'Tierra'" << endl;
 // cout << 0 << " "<< 0 << endl <<'e'<< endl ;
 // cout << x1 << " "<< y1 << endl <<'e'<< endl << flush;

  RK3(x1,x2,y1,y2,t);
 }
 archivo3.close();
 prop.close();

 return 0;
}
 
[$[Get Code]]

Animation (python + matplotlib)

#!/usr/local/bin/python
#***********************************************************************#
#*                      TRAJECTORY ANIMATION                           *#
#*                                                                     *#
#* This program reads the X-Y trajectory of a particle an generates    *#
#* an animation of the motion.                                         *#
#*                                                                     *#
#***********************************************************************#
 # AUTHOR: FELIPE GONZALEZ CATALDO, September 2018.
from pylab import *

fig = figure(1)
ax = subplot(111)

data = loadtxt('sol-tierraRK3.dat',usecols=(0,1,2,3,4)) # t, x, vx, y, vy
x= data[:,1]
y= data[:,3]

xlim(-2,2)
ylim(-2,2)
sun,        = ax.plot([0],[0], 'oy',ms=50)
planet,     = ax.plot([0],[0], 'or',ms=10)
trajectory, = ax.plot([0],[0],'--')
show(block=False)


for i in xrange(len(data)):
 planet.set_xdata( x[i] )
 planet.set_ydata( y[i] )
 trajectory.set_xdata( x[0:i] )
 trajectory.set_ydata( y[0:i] )
 plt.pause(1e-30)
 draw()

 #savefig(str(i)+'.png')
 
[$[Get Code]]

Code (python)

#!/usr/bin/python
#***********************************************************************#
#*                      SUN - EARTH ORBIT                              *#
#*                                                                     *#
#* This program solves the differential equation                       *#
#*                        m R''(t) = - GMm/r² r^                       *#
#* where R=(x,y) and r^ = (x,y)/sqrt(x^2+y^2)  using Runge-Kutta       *#
#* methods.                                                            *#
#*                                                                     *#
#***********************************************************************#
 # AUTHOR: FELIPE GONZALEZ CATALDO, September 2018.

from pylab import *
# -*- coding: utf-8 -*-


G=0.00011859645   # in AU^3/(earthmass*year^2)
m=1.00            # earthmass
M=332946.05       # sunmass=332946.05 earthmass
tau=0.01; tmax=5  # year



def fx1(x1,x2,y1,y2,t): return x2
def fy1(x1,x2,y1,y2,t): return y2
def fx2(x1,x2,y1,y2,t): return -G*M*x1/(x1*x1+y1*y1)**1.5
def fy2(x1,x2,y1,y2,t): return -G*M*y1/(x1*x1+y1*y1)**1.5

def RK3(x1,x2,y1,y2,t):
 k1x1 = tau*fx1(x1,x2,y1,y2,t)
 k1x2 = tau*fx2(x1,x2,y1,y2,t)
 k1y1 = tau*fy1(x1,x2,y1,y2,t)
 k1y2 = tau*fy2(x1,x2,y1,y2,t)

 k2x1 = tau*fx1(x1+0.5*k1x1, x2+0.5*k1x2, y1+0.5*k1y1, y2+0.5*k1y2, t+0.5*tau)
 k2x2 = tau*fx2(x1+0.5*k1x1, x2+0.5*k1x2, y1+0.5*k1y1, y2+0.5*k1y2, t+0.5*tau)
 k2y1 = tau*fy1(x1+0.5*k1x1, x2+0.5*k1x2, y1+0.5*k1y1, y2+0.5*k1y2, t+0.5*tau)
 k2y2 = tau*fy2(x1+0.5*k1x1, x2+0.5*k1x2, y1+0.5*k1y1, y2+0.5*k1y2, t+0.5*tau)

 k3x1 = tau*fx1(x1-k1x1+2*k2x1, x2-k1x2+2*k2x2, y1-k1y1+2*k2y1, y2-k1y2+2*k2y2, t+tau)
 k3x2 = tau*fx2(x1-k1x1+2*k2x1, x2-k1x2+2*k2x2, y1-k1y1+2*k2y1, y2-k1y2+2*k2y2, t+tau)
 k3y1 = tau*fy1(x1-k1x1+2*k2x1, x2-k1x2+2*k2x2, y1-k1y1+2*k2y1, y2-k1y2+2*k2y2, t+tau)
 k3y2 = tau*fy2(x1-k1x1+2*k2x1, x2-k1x2+2*k2x2, y1-k1y1+2*k2y1, y2-k1y2+2*k2y2, t+tau)

 x1 = x1 +(k1x1+4*k2x1+k3x1)/6.0
 x2 = x2 +(k1x2+4*k2x2+k3x2)/6.0
 y1 = y1 +(k1y1+4*k2y1+k3y1)/6.0
 y2 = y2 +(k1y2+4*k2y2+k3y2)/6.0

 return x1,x2,y1,y2

def KineticEnergy(x1, x2, y1, y2):
 return 0.5*m*(x2*x2+y2*y2)        #  in earthmass*(AU/year)^2

def PotentialEnergy(x1, x2, y1, y2):
  return -G*M*m/sqrt(x1*x1+y1*y1)    # in earthmass*(AU/year)^2

#-------------------#
#    ANIMATION      #
#-------------------#
fig = figure(1)
ax = subplot(111)
xlim(-2,2)
ylim(-2,2)
sun,        = ax.plot([0],[0], 'oy',ms=50)
planet,     = ax.plot([0],[0], 'or',ms=10)
trajectory, = ax.plot([0],[0],'--')
show(block=False)



#-------------------#
#   MAIN PROGRAM    #
#-------------------#
t=0; x1=1; x2=0; y1=0; y2=7.28   # Initial conditions
for t in arange(0,tmax,tau):

 x1,x2,y1,y2 = RK3(x1,x2,y1,y2,t)
 planet.set_xdata( x1 )
 planet.set_ydata( y1 )
 plt.pause(1e-30)
 draw()

 # Print the relevant data
 K = KineticEnergy(x1,x2,y1,y2)
 P = PotentialEnergy(x1,x2,y1,y2)
 #print "t[year]= %2.4f  x[AU]= %8.4f  y[AU]= %8.4f  vx[AU/year]= %8.4f  vy[AU/year]= %8.4f  Kin[ME*(AU/year)^2]= %8.4f  Pot[ME*(AU/year)^2]= %8.4f"  % (t,x1,y1,x2,y2, K,P)

 legend([planet],[r'$t=$'+str(t)],  numpoints=1)
 #savefig('Energies-vs-Time.png')

 
[$[Get Code]]

Code simplified (python)

Using numpy arrays, the code can be written in a more compact and simplified version:


#!/usr/bin/python
#***********************************************************************#
#*                      SUN - EARTH ORBIT                              *#
#*                                                                     *#
#* This program solves the differential equation                       *#
#*                        m R''(t) = - GMm/r^2 r^                      *#
#* where R=(x,y) and r^ = (x,y)/sqrt(x^2+y^2)  using Runge-Kutta       *#
#* methods.                                                            *#
#*                                                                     *#
#***********************************************************************#
 # AUTHOR: FELIPE GONZALEZ CATALDO, September 2018.

from pylab import *
# -*- coding: utf-8 -*-



G=0.00011859645   # in AU^3/(earthmass*year^2)
m=1.00            # earthmass
M=332946.05       # sunmass=332946.05 earthmass
tau=0.01; tmax=5  # year


def f1(r,v,t): return v
def f2(r,v,t): return -G*M*r/norm(r)**3

def RK3(r,v,t):
 k11 = tau*f1(r,v,t)
 k12 = tau*f2(r,v,t)

 k21 = tau*f1(r+0.5*k11, v+0.5*k12, t+0.5*tau)
 k22 = tau*f2(r+0.5*k11, v+0.5*k12, t+0.5*tau)

 k31 = tau*f1(r-k11+2*k21, v-k12+2*k22, t+0.5*tau)
 k32 = tau*f2(r-k11+2*k21, v-k12+2*k22, t+0.5*tau)

 r = r + (k11+4*k21+k31)/6.0
 v = v + (k12+4*k22+k32)/6.0

 return r,v

def KineticEnergy(r,v):
 return 0.5*m*norm(v)**2        #  in earthmass*(AU/year)^2

def PotentialEnergy(r,v):
  return -G*M*m/norm(r)    # in earthmass*(AU/year)^2

#-------------------#
#    ANIMATION      #
#-------------------#
fig = figure(1)
ax = subplot(111)
xlim(-2,2)
ylim(-2,2)
sun,        = ax.plot([0],[0], 'oy',ms=50)
planet,     = ax.plot([0],[0], 'or',ms=10)
trajectory, = ax.plot([0],[0],'--')
show(block=False)



#-------------------#
#   MAIN PROGRAM    #
#-------------------#
t=0; r = np.array([1.0,0.0]); v = np.array([0,7.28])   # Initial conditions
for t in arange(0,tmax,tau):

 r,v = RK3(r,v,t)
 planet.set_xdata( r[0] )
 planet.set_ydata( r[1] )
 plt.pause(1e-30)
 draw()

 # Print the relevant data
 K = KineticEnergy(r,v)
 P = PotentialEnergy(r,v)
 print "t[year]= %2.4f  x[AU]= %8.4f  y[AU]= %8.4f  vx[AU/year]= %8.4f  vy[AU/year]= %8.4f  Kin[ME*(AU/year)^2]= %8.4f  Pot[ME*(AU/year)^2]= %8.4f"  % (t,r[0],r[1],v[0],v[1], K,P)

 legend([planet],[r'$t=$'+str(t)],  numpoints=1)
 #savefig('Energies-vs-Time.png')
 
[$[Get Code]]