Felipe Gonzalez Web Page Programas/Ecuación De Difusion

Programas

Ecuación De Difusion

La ecuación de difusión permite describir la dinámica de un sistema difusivo, como la temperatura en un material, el movimiento de una tinta en agua, e incluso la propagación de células cancerígenas en el cerebro. A continuación veremos algunas aplicaciones de esta ecuación:

$\frac{\partial\phi(\mathbf{r},t)}{\partial t} = \nabla \cdot \big[ D(\phi,\mathbf{r}) \nabla\phi(\mathbf{r},t) \big].$

EJEMPLOS

Ecuación de difusión 1D: enfriando una barra por los extremos
Modelo de crecimiento de un tumor

Ecuación de difusión 1D

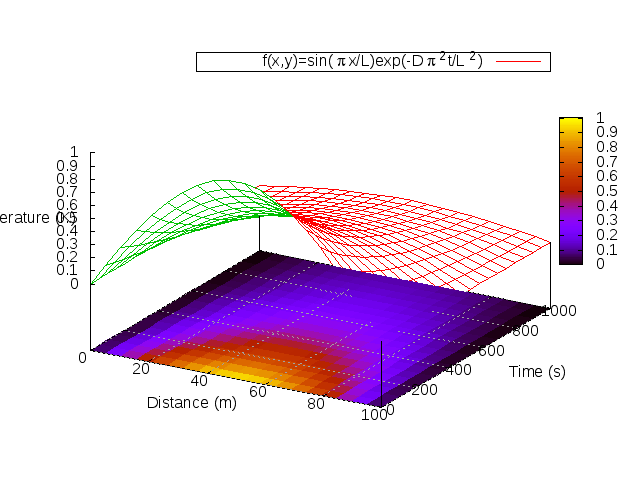
El problema más sencillo en donde aparece la ecuación de difusión es en la propagación del calor en una barra unidimensional de largo $L$ , sujeta a las condiciones de borde $T(0,t)=T_1$ y $T(L,t)=T_2$ , donde $T(x,t)$ es la temperatura a una distancia $x$ del borde izquierdo en un tiempo $t$ . Si el coeficiente de difusión es constante (la barra es homogénea), entonces podemos escribir la ecuación de difusión como

$\frac{\partial T(x,t)}{\partial t} = D\, \nabla^2 T(x,t),$

donde $D$ es el coeficiente de difusión que caracteriza al material del cual la barra está hecho. Para el caso particular en que mantenemos los bordes fríos ( $T(0,t)=0$ , $T(L,t)=0$ ) y un perfil inicial $T(x,0)=\sin(\pi x/L)$ , se puede resolver el problema analíticamente, y la solución es

$T(x,t) = \sin\left(\frac{\pi x}{L}\right)\exp\left(-\frac{D \pi^2 t}{L^2}\right).$

Podemos resolver numéricamente la ecuación de difusión mediante diferencias finitas, usando el esquema FTCS:

$\frac{T_j^{n+1}-T_j^n}{\Delta t}=D\frac{T_{j+1}^n-2T_j^n+T_{j-1}^n}{(\Delta x)^2},$

que podemos reescribir como

$T_j^{n+1}=T_j^n+D\,r(T_{j+1}^n-2T_{j}^n+\,T_{j-1}^n),$ ,

donde $T_j^n=T(x_j,t_n)$ es la temperatura en la posición $x_j=j \Delta x$ en el tiempo $t_n=n\Delta t$ , y $r=\Delta t/(\Delta x)^2$ . Aquí, $\Delta x=L/(N-1)$ es el tamaño de las $N$ divisiones (de $0$ a $N-1$ ) del intervalo $\left[0,L\right]$ , de modo que $x_0=0$ y $x_{N-1}=L$ ; mientras que $\Delta t$ es el paso de tiempo, que debe cumplir la restricción de convergencia numérica

$2D\Delta t \leq \Delta x^2$ .

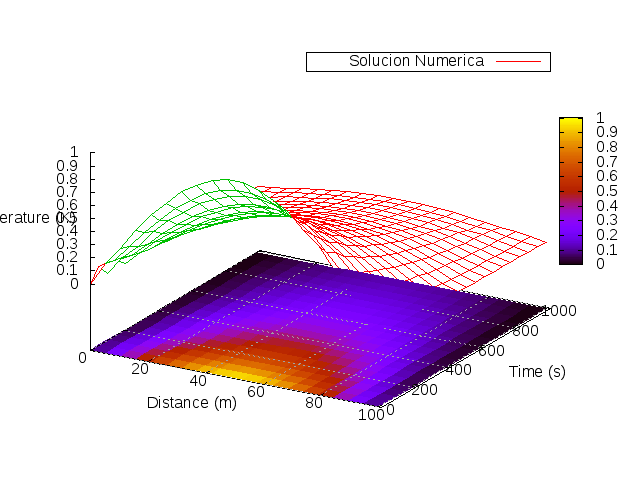
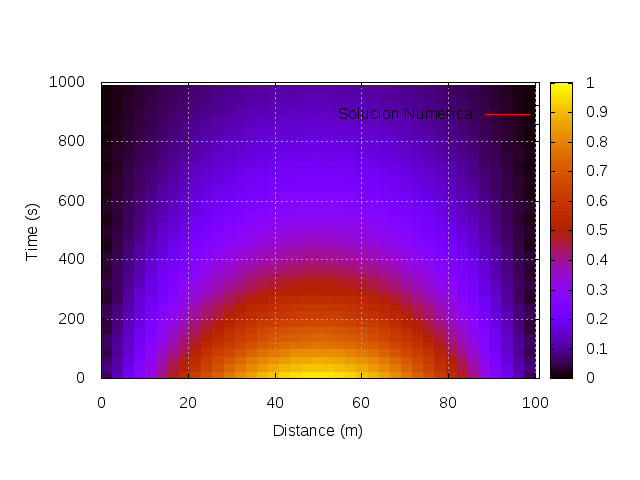
De esta manera, podemos llegar a la misma solución analítica, y luego resolver problemas más complicados, sin solución analítica. Mostramos a continuación la solución analítica versus la solución numérica:

Código (C++)

#include<iostream>
#include<fstream>
#include<cmath>
using namespace std;

//const double D=2.2;
const int Ndx=70, tmax=1000; // segundos
const double L=100.0; // metros
const double Tmax=5; // Kelvin
const double dx=L/(Ndx-1), dt=0.9*(dx*dx/(2.0*3.2)), r=dt/(dx*dx);

// Coeficiente de difusion
double D(double x)
{
// double Dx = (x<L/2.0)? 3.2 : 0.2; // metros²/segundo
double Dx = 2.2;
return Dx;
}

// Condicion de Borde 1: T(0,t)=g1(t)
//double g1(double t){ return 1+500*exp(-0.001*(t-100)*(t-100));}
//double g1(double t){ return 1+(Tmax-1)*(2*atan(t/100)/M_PI);}
double g1(double t){ return 0.0;}
// Condicion de Borde 2: T(L,t)=g2(t)
double g2(double t){ return 0.0;}
// Condicion Inicial: T(x,0)=f(x) (Se debe cumplir f(0)=T(0,0)=g1(0) y f(L)=T(L,0)=g2(0))
double f(double x){ return sin(M_PI*x/L);}

int main()
{
double T[Ndx]; // T(x,t)
double Tant[Ndx]; // T(x,t) (copia)
for (int j=0; j<Ndx; j++) T[j]=0;

// Condicion inical
for (int j=0; j<Ndx-1; j++) T[j]=f(j*dx);

ofstream arch("calor.dat");
arch << "#x" << "\t" << "#t" << "\t" << "T(x,t)" << endl;

for (double t=0; t<=tmax; t+=dt)
{
if (int(t/dt)%50==0)
{
/* DIBUJO GNUPLOT */
cout<<"plot [0:"<<L<<"][0:" << Tmax << "]";
cout << " '-' w l ls 3 lw 8 t 'D=3.2',"; // Puntos para la barra
cout << " '-' w l ls 2 lw 8 t 'D=1.2',"; // Puntos para la barra
cout << " '-' ls 2 lc 0 t 'Time: t=" << t << "'" << endl; // Puntos T(x,t)
cout << "0 0" << endl << L/2 << " 0" << endl; // La barra va de (0,0) a (L/2,0)
cout << 'e' << endl; // Terminamos los 2 puntos que definen la barra.
cout << L/2 << " 0" << endl << L << " 0" << endl; // La barra va de (0,0) a (L/2,0)
cout << 'e' << endl; // Terminamos los 2 puntos que definen la barra.
for (int j=0; j<Ndx; j++)
{
arch << j*dx << " " << t << " " << T[j] << endl;
cout << j*dx << " " << T[j] << endl;
}
cout << 'e' << endl << flush;
}
// Aplicando condiciones de Borde
T[0]=g1(t);
T[Ndx-1]=g2(t);
// Haciendo una copia del arreglo
for(int j=0; j<Ndx; j++) Tant[j]=T[j];
// Resolviendo entre medio
for (int j=1; j<Ndx-1; j++)
{
T[j]=Tant[j] + D(j*dx)*r*(Tant[j+1]-2*Tant[j]+Tant[j-1]);
}
}
cout << "pause 2" << endl;
arch.close();
return 0;
}

[$[Get Code]]

Compilado el programa, ejecutar con

./programa | gnuplot

[$[Get Code]]

Código (python)

from pylab import *
from numpy import *
Ndx=70; tmax=50; # segundos
L=100.0; # metros
Tmax=5.0; # Kelvin
D=20.0
dx=L/(Ndx-1); dt=0.8*(dx*dx/(2.0*D)); r=dt/(dx*dx)
Temp = []

# Condicion de Borde 1: T(0,t)=g1(t)
def g1(t): return 0.0
# Condicion de Borde 2: T(L,t)=g2(t)
def g2(t): return 0.0
# Condicion Inicial: T(x,0)=f(x) (Se debe cumplir f(0)=T(0,0)=g1(0) y f(L)=T(L,0)=g2(0))
def f(x): return Tmax*sin(pi*x/L);

T = [0.0]*Ndx # T(x,t)
Tant = [0.0]*Ndx # T(x,t) (copia)
# Condicion inical
for j in xrange(Ndx-1): T[j]=f(j*dx)
#print "#x","#t","#T(x,t)"

for n in xrange(int(tmax/dt)):
# Aplicando condiciones de Borde
t=n*dt
T[0]=g1(t)
T[Ndx-1]=g2(t)
# Haciendo una copia del arreglo
Tant=list(T)
# Resolviendo entre medio
for j in xrange(Ndx-1):
T[j]=Tant[j] + D*r*(Tant[j+1]-2*Tant[j]+Tant[j-1])

# Cada 10 pasos...
if (int(t/dt)%10==0):
# Anadimos al arreglo de temperaturas la lista de temperaturas en este paso
Temp += [ list(T) ]
# for j in xrange(Ndx):
# print j*dx, t, T[j]
Temp = array(Temp)

from mpl_toolkits.mplot3d.axes3d import get_test_data
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1, projection='3d')
X = array([j*dx for j in xrange(Ndx)] )
Y = array([n*dt for n in xrange(len(Temp))] )
X, Y = meshgrid(X, Y)
Z = Temp
surf = ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=cm.coolwarm, vmin=0, vmax=Tmax, linewidth=0, antialiased=False)
ax.set_zlim3d(0, Tmax)

show()

[$[Get Code]]

Modelo de crecimiento de un tumor

Existen varios modelos que permiten estudiar el crecimiento de un tumor. Uno de los modelos más simples para modelar la evolución de un glioblastoma en presencia de quimioterapia se puede formular postulando que la tasa de crecimiento de células cancerígenas tiene un término difusivo y uno de crecimiento poblacional, es decir,

$\frac{\partial c}{\partial t} = \nabla\cdot (D \nabla c) + \rho c - G(t)c,$

donde $c=c(\vec r, t)$ es la concentración de células tumorales en un sitio $\vec r$ en un tiempo $t$ , y $G(t)$ es una función que describe los efectos de la quimioterapia. El coeficiente de difusión $D$ en general depende de la concentración de células cancerígenas $c$ , es decir, $D=D(c(\vec r,t))$ .

Si suponemos simetría esférica, podemos expresar la ecuación anterior como

$\frac{\partial c}{\partial t}$

$=$

$\frac{\partial D}{\partial r}+\frac{\partial D}{\partial c}\frac{\partial c}{\partial r}$

$+$

$D(c)\left(\frac{\partial^2 c}{\partial r^2}+\frac{1}{r}\frac{\partial c}{\partial r}\right) + \rho c - G(t)c$

Para este caso particular, vamos a elegir

$D(c)=D_{min}+ \frac{2}{\pi}(D_{max}-D_{min})\arctan(c)$ ,

de modo que $D=D_{min}$ en zonas donde $c=0$ , y vale a lo más $D_{max}$ cuando la concentración es muy grande. Resolvemos la ecuación usando diferencias finitas, tal como suele resolverse la ecuación de difusión.

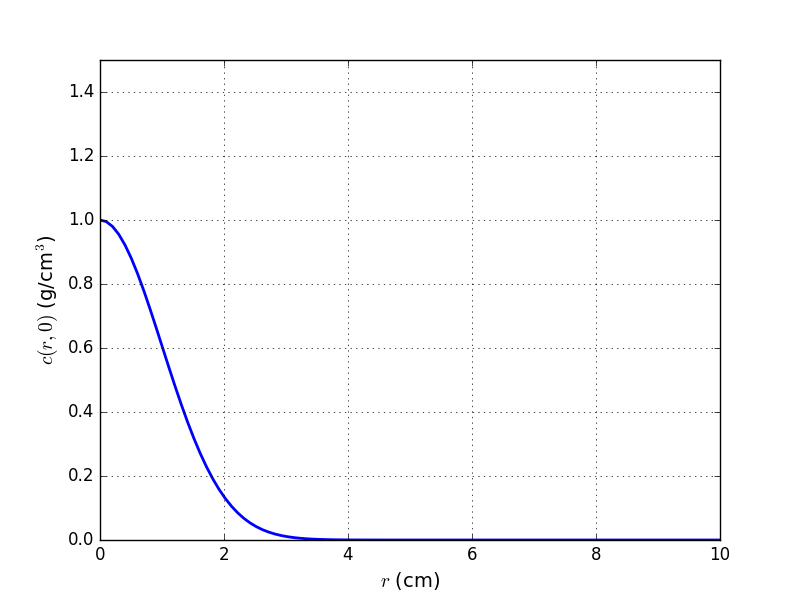
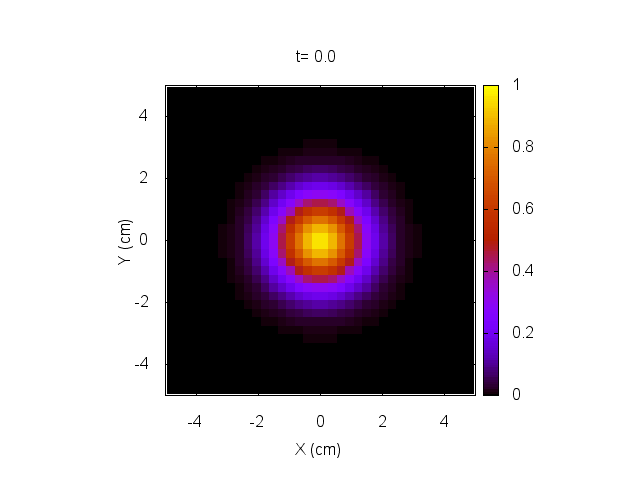
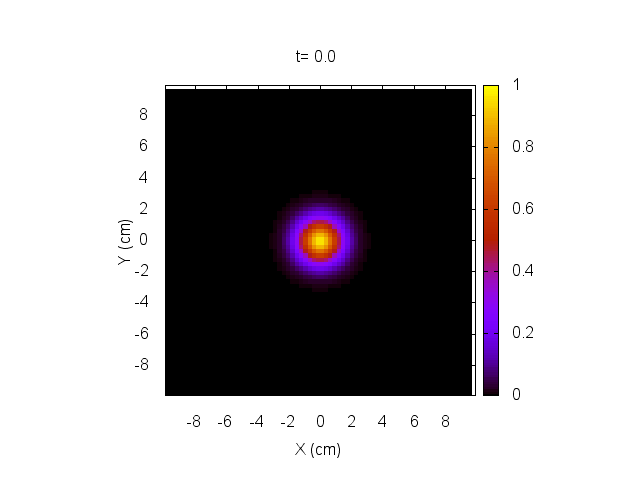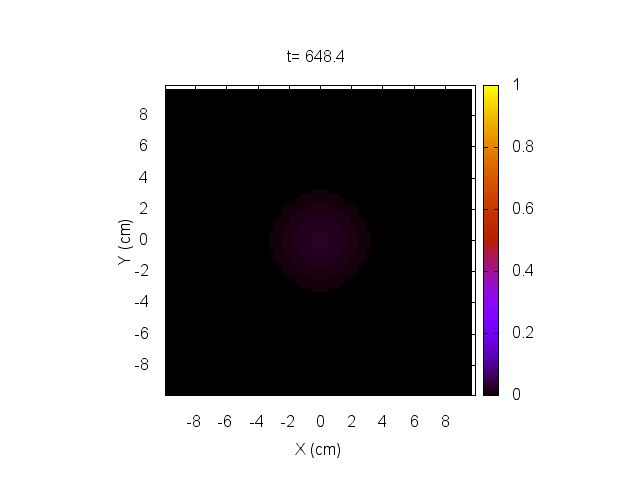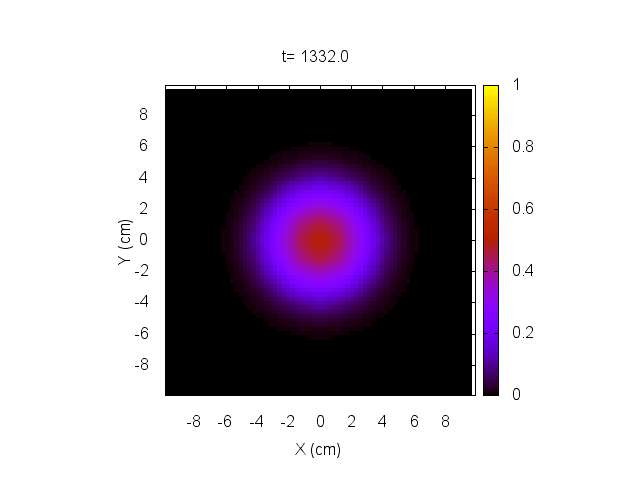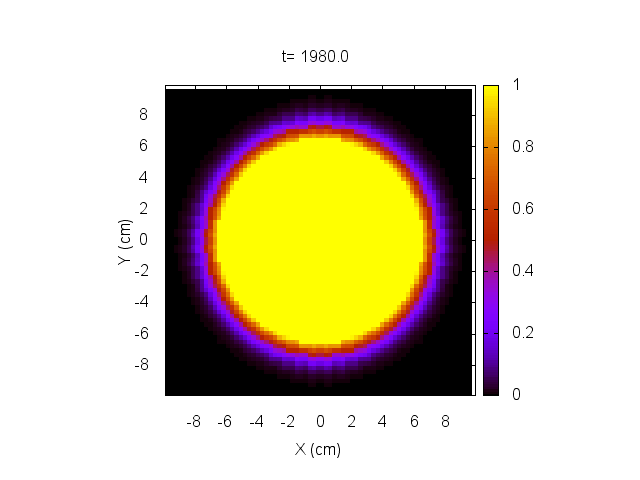
Para comenzar, daremos una condición inicial correspondiente a un tumor localizado en el centro del cerebro, como muestran las figuras a continuación.

Usando un tratamiento representado por dos pulsos a los 200 y 500 segundos, dados por

$G(t) = 10\rho\exp\left(-\frac{(t-200)^2}{1000}\right)+10\rho\exp\left(-\frac{(t-500)^2}{1000}\right)$

hacemos evolucionar el sistema y lo mostramos a continuación.

En este caso, el tratamiento $G(t)$ no es capaz de eliminar el tumor, el cual sigue creciendo sin control.

Código (python)

#***********************************************************************#
#* ECUACION DE CRECIMIENTO DE UN TUMOR CEREBRAL *#
#* *#
#* Este programa encuentra la solucion a una de las ecuaciones *#
#* propuestas para la propagacion de un tumor, tomada del *#
#* trabajo de Tiberiu Harko y M. K. Mak: *#
#* TRAVELLING WAVE SOLUTIONS OF THE REACTION-DIFFUSION MATHEMATICAL *#
#* MODEL OF GLIOBLASTOMA GROWTH: AN ABEL EQUATION BASED APPROACH: *#
#* dc/dt = V.(D Vc) + rho*c - G(t)c *#
#* donde c=c(r,t) es la densidad de celulas tumorales en la *#
#* posicion r en tiempo t, rho la tasa neta de proliferacion, *#
#* y D=D(c(r)), el coef. de difusion, que depende de c. *#
#* G(t) es una funcion de influencia externa, que representa el *#
#* efecto de la quimioterapia. *#
#* *#
#* Suponiendo simetria radial, se obtiene *#
#* dc/dt = D'(c(r))*(dc/dr)^2 + D(c(r))*d^2c/dr^2 + rho*c - G(t)c *#
#***********************************************************************#
# AUTOR: FELIPE GONZALEZ CATALDO, Octubre 2015.

from numpy import *
R=9.9 # Radio del cerebro (cm)
N=100 # Divisiones del intervalo [0,R]
Dmax=0.010 # Maximo coeficiente de difusion (ver D abajo), en cm^2/sec
Dmin=0.001 # Minimo coeficiente de difusion (ver D abajo), en cm^2/sec
rho=0.005 # rho= tasa neta de proliferacion, en 1/sec
dr=R/(N-1)
dt=0.8*dr*dr/(2*Dmax) # Mientras mas grande la difusion, mas chico debe ser dt
t=0.0; tmax=2000.0
c = [0.0]*N
c_ant = [0.0]*N

# Coeficiente de difusion:
def D(c,r):
return Dmin+ 0.63661977*(Dmax-Dmin)*arctan(c) # 2/pi=0.6366

# Derivada parcial del coef. de difusion respecto a c (derivar arriba):
def Dc(c,r):
return 0.63661977*(Dmax-Dmin)/(1+c*c)

# Derivada parcial del coef. de difusion respecto a r (derivar arriba):
def Dr(c,r):
return 0.0

# Condicion inicial c(r,0)=f(r)
def f(r):
return exp(-50*(r/R)**2) if r<R/2.0 else 0.0

# When chemotherapy is administered, G(t) is constant, and G(t) = 0 otherwise
def G(t):
return 10*rho*exp(-(t-200)**2/1000)+10*rho*exp(-(t-500)**2/1000) #+100*rho*exp(-(t-2000)**2/1000)

def PrintForGnuplot(u):
# Con esta funcion imprimimos la funcion para gnuplot: r, c(r)
print "plot [0:",R,"][0:5] '-' w l ls 12 lw 3 title 't=", t,"'"
for j in xrange(N):
print j*dr, c[j]
print "end"
print "set grid"
# print "pause",1

def PrintContoursGnuplot(u):
# Con esta funcion imprimimos un mapa de contornos pm3d map de gnuplot
# print "set isosample 10,10"
print "set dgrid3d 31,31,31"
print "set pm3d map"
print "set cbrange [0:1]"
print "set title 't=", t,"'"
print "splot [-"+str(R)+":"+str(R)+"][-"+str(R)+":"+str(R)+"][] '-' title 't=", t,"'"
No = 15
do = 2.0*pi/No
for i in xrange(No):
for j in xrange(N):
x=j*dr*cos(i*do);
y=j*dr*sin(i*do);
print x, y , c[j]
print "e"
# print "set grid"

# Condicion inicial c(r,0)=f(r)
for j in xrange(N):
c[j]=f(j*dr);
c_ant[j]=f(j*dr);

interval = int(tmax/dt/500)
while(t<=tmax):
# if int(t/dt)%interval==0: PrintForGnuplot(c)
if int(t/dt)%(interval*20)==0: PrintContoursGnuplot(c)

#*** METODO PREDICTOR ****#
# Primero los bordes
c[0] = c_ant[0] + dt*( D(c_ant[0],0*dr)*(4.0*(c_ant[1]-c_ant[0])/(dr*dr)) )
c[0] += dt*( rho*c_ant[0] - G(t)*c_ant[0] )
c[N-1]=0.0 # c(R)=0
# Luego entre medio
for j in xrange(1,N-1):
dcdr = (c_ant[j+1]-c_ant[j-1])/(2.0*dr)
c[j] = c_ant[j] + dt*( dcdr*( Dr(c_ant[j],j*dr) + Dc(c_ant[j],j*dr)*dcdr ) )
c[j] += dt*( D(c_ant[j],j*dr)*(c_ant[j+1]-2*c_ant[j]+c_ant[j-1])/(dr*dr) )
c[j] += dt*( D(c_ant[j],j*dr)*dcdr/(j*dr) )
c[j] += dt*( rho*c_ant[j] - G(t)*c_ant[j] )
#************************#
# Guardamos las posiciones nuevas para la vuelta siguiente
c_ant = list(c)
t+=dt
# >>END OF WHILE<<

[$[Get Code]]

« Programas

Felipe Gonzalez Web Page

Ecuación De Difusion

Código (C++)

Código (python)

Código (python)

Search

Options: